(本題16分)已知函數(shù)
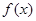
滿足滿足
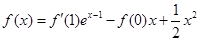
;
(1)求
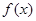
的解析式及單調(diào)區(qū)間;
(2)若
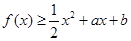
,求
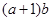
的最大值.
(1)
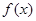
的解析式為
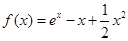
,單調(diào)遞增區(qū)間為
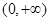
,單調(diào)遞減區(qū)間為
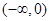
;(2)
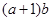
的最大值為
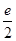
利用導數(shù)與函數(shù)單調(diào)性的關系求解單調(diào)區(qū)間以及利用導數(shù)求解函數(shù)的最值求解。
試題分析:
(1)
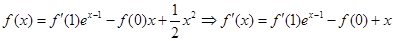
令
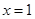
得:
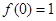
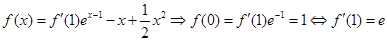
得:
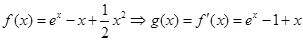
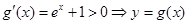
在
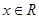
上單調(diào)遞增
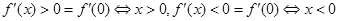
得:
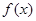
的解析式為
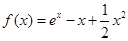
且單調(diào)遞增區(qū)間為
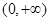
,單調(diào)遞減區(qū)間為
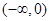
……………8分
(2)
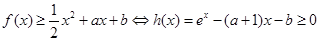
得
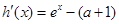
①當
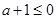
時,
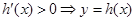
在
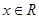
上單調(diào)遞增
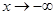
時,
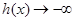
與
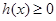
矛盾
②當
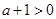
時,
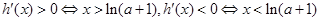
得:當
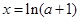
時,
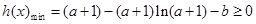
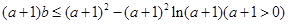
令
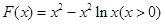
;則
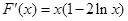
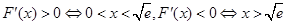
當
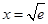
時,
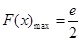
當
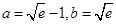
時,
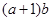
的最大值為
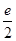
………………………16分
點評:解決此題的關鍵是熟練掌握利用導數(shù)與函數(shù)單調(diào)性的關系求解單調(diào)區(qū)間以及利用導數(shù)求解函數(shù)的最值的方法,以及較強的邏輯推理、運算求解及轉(zhuǎn)化能力,難度很大。
練習冊系列答案
相關習題
科目:高中數(shù)學
來源:不詳
題型:解答題
已知函數(shù)f(x)=(x
2+ax+2)e
x,(x,a∈R).
(1)當a=0時,求函數(shù)f(x)的圖象在點A(1,f(1))處的切線方程;
(2)若函數(shù)y=f(x)為單調(diào)函數(shù),求實數(shù)a的取值范圍;
(3)當

時,求函數(shù)f(x)的極小值.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
已知函數(shù)
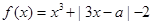
在
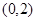
上恰有兩個零點,則實數(shù)
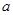
的取值范圍為( )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
設
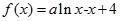
,(
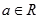
),曲線
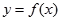
在點
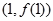
處的切線垂直于
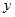
軸.
(Ⅰ) 求
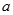
的值;
(Ⅱ) 求函數(shù)
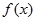
的極值.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
導函數(shù)

在[-2,2]上的最大值為( )
A. | B.16 | C.0 | D.5 |
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
已知函數(shù)
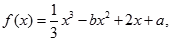
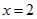
是
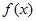
的一個極值點.
(Ⅰ)求函數(shù)
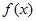
的單調(diào)區(qū)間;
(Ⅱ)若當
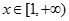
時,
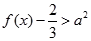
恒成立,求
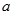
的取值范圍。
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
(本題12分)
已知函
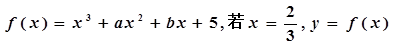
有極值,且曲線
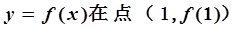
處的切線斜率為3.
(1)求函數(shù)
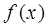
的解析式;
(2)求
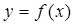
在[-4,1]上的最大值和最小值。
(3)函數(shù)
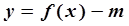
有三個零點,求實數(shù)
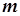
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
一物體沿直線以
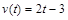
(
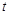
的單位:秒,
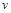
的單位:米/秒)的速度做變速直線運動,則該物體從時刻
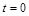
到5秒運動的路程
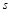
為
米.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
曲線
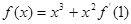
在點
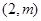
處的切線斜率為
.
查看答案和解析>>

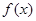 滿足滿足
滿足滿足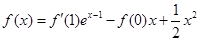 ;
;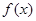 的解析式及單調(diào)區(qū)間;
的解析式及單調(diào)區(qū)間;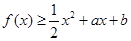 ,求
,求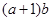 的最大值.
的最大值.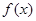 的解析式為
的解析式為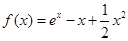 ,單調(diào)遞增區(qū)間為
,單調(diào)遞增區(qū)間為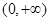 ,單調(diào)遞減區(qū)間為
,單調(diào)遞減區(qū)間為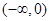 ;(2)
;(2)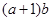 的最大值為
的最大值為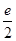
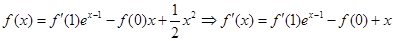
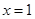 得:
得: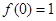
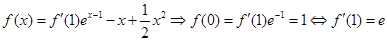
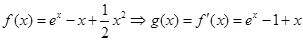
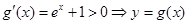 在
在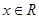 上單調(diào)遞增
上單調(diào)遞增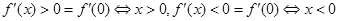
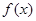 的解析式為
的解析式為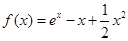
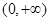 ,單調(diào)遞減區(qū)間為
,單調(diào)遞減區(qū)間為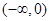 ……………8分
……………8分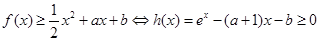 得
得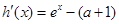
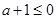 時,
時,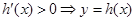 在
在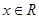 上單調(diào)遞增
上單調(diào)遞增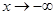 時,
時,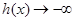 與
與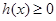 矛盾
矛盾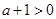 時,
時,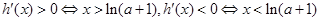
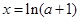 時,
時,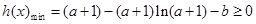
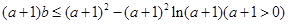
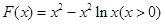 ;則
;則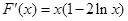
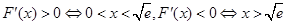
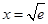 時,
時,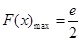
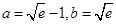 時,
時,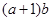 的最大值為
的最大值為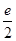 ………………………16分
………………………16分

 時,求函數(shù)f(x)的極小值.
時,求函數(shù)f(x)的極小值.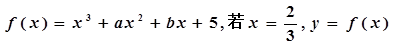 有極值,且曲線
有極值,且曲線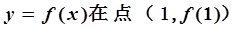 處的切線斜率為3.
處的切線斜率為3.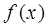 的解析式;
的解析式;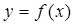 在[-4,1]上的最大值和最小值。
在[-4,1]上的最大值和最小值。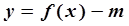 有三個零點,求實數(shù)
有三個零點,求實數(shù)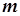 的取值范圍.
的取值范圍.