【答案】
分析:(I)根據兩數相除異號得負的取符號法則,得到2x+1與x-1異號,可化為兩個一元一次不等式組,分別求出兩不等式組的解集,即可得到原不等式的解集;
(II)把原已知的雙向不等式化為不等式組,把不等式①及不等式②分別化為不等式組,求出不等式組交集的并集確定出不等式①和不等式②的解集,求出兩不等式解集的交集,即為原不等式的解集.
解答:(本小題12分)
解:(I)原不等式可以化為
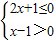
或
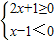
,(2分)
解得:
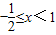
,(4分)
則不等式的解集為
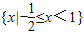
;(5分)
(II)原不等式可以化為
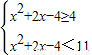
,(7分)
即
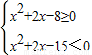
,(8分)
∴
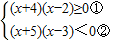
,
不等式①可化為:
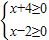
或
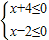
,
解得:x≤-4或x≥2;
不等式②可化為:
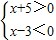
或
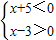
,
解得:-5<x<3,(10分)
取兩解集的公共部分得:-5<x≤-4或2≤x<3.(11分)
則不等式的解集為{x|-5<x≤-4或2≤x<3}.(12分)
點評:此題考查了其他不等式的解法,以及一元二次不等式解法,利用了轉化的思想,其中轉化的理論依據為兩數相乘,同號得正、異號得負的取符號法則.靈活運用轉化思想是解本題的關鍵.

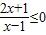 (II)4≤x2+2x-4<11.
(II)4≤x2+2x-4<11.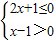 或
或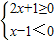 ,(2分)
,(2分)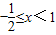 ,(4分)
,(4分)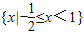 ;(5分)
;(5分)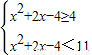 ,(7分)
,(7分)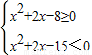 ,(8分)
,(8分)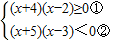 ,
,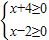 或
或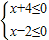 ,
,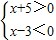 或
或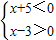 ,
,
