
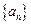 滿足
滿足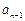 +
+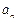 =4n-3(n∈
=4n-3(n∈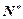 ).
).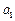 =2,求數列
=2,求數列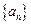 的前n項和
的前n項和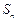 ;
;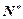 ,都有
,都有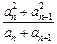 ≥5成立,求
≥5成立,求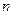 為偶數時,
為偶數時,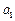 的取值范圍.
的取值范圍.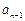 +
+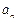 =4n-3(n∈
=4n-3(n∈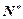 )得
)得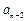 +
+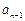 =4n+1(n∈
=4n+1(n∈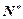 ).
).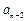 -
-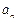 =4.
=4. 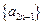 是首項為
是首項為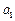 ,公差為4的等差數列;數列
,公差為4的等差數列;數列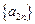 是首項為
是首項為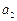 ,公差為4的等差數列. …………………………. ………………………………………………2分
,公差為4的等差數列. …………………………. ………………………………………………2分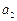 +
+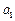 =1,
=1,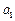 =2,得
=2,得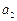 =-1.
=-1.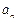 =
=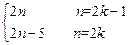 (k∈Z).……. ……………………………………………3分
(k∈Z).……. ……………………………………………3分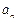 =2n,
=2n,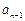 =2n-3,
=2n-3,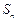 =
=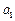 +
+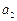 +
+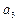 +…+
+…+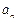 =(
=(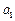 +
+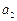 )+(
)+(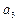 +
+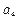 )+…+(
)+…+(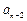 +
+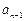 )+
)+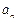
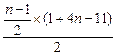 +2n=
+2n=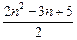 .
.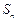 =
=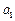 +
+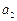 +
+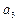 +…+
+…+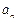 =(
=(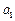 +
+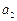 )+(
)+(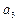 +
+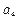 )+…+(
)+…+(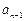 +
+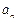 )
)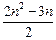 .
.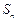 =
=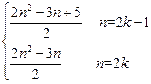 (k∈Z).……………………………………………7分
(k∈Z).……………………………………………7分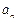 =
=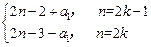 (k∈Z).
(k∈Z).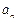 =2n-3-
=2n-3-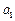 ,
,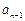 =2n+
=2n+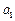 .
.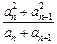 ≥5,得
≥5,得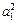 +
+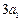 ≥
≥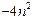 +16n-12. ……………………………………9分
+16n-12. ……………………………………9分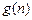 =
=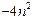 +16n-12=
+16n-12=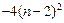 +4.
+4.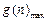 =4,所以
=4,所以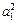 +
+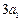 ≥4.
≥4.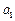 ≥1或
≥1或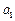 ≤-4. ………………………………………………………11分
≤-4. ………………………………………………………11分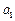 的取值范圍是
的取值范圍是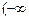 ,
,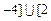 ,
,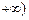 .……………………………………12分
.……………………………………12分

 中考利劍中考試卷匯編系列答案
中考利劍中考試卷匯編系列答案 教育世家狀元卷系列答案
教育世家狀元卷系列答案 黃岡課堂作業本系列答案
黃岡課堂作業本系列答案 單元加期末復習先鋒大考卷系列答案
單元加期末復習先鋒大考卷系列答案科目:高中數學 來源:不詳 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com