
已知各項均為正數的數列 中,
中, 是數列
是數列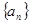 的前
的前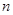 項和,對任意
項和,對任意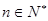 ,有
,有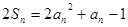 .函數
.函數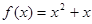 ,數列
,數列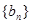 的首項
的首項

(Ⅰ)求數列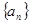 的通項公式;(Ⅱ)令
的通項公式;(Ⅱ)令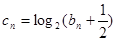 求證:
求證: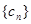 是等比數列并求
是等比數列并求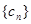 通項公式
通項公式
(Ⅲ)令 ,
, ,求數列
,求數列 的前n項和
的前n項和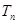 .
.
(Ⅰ)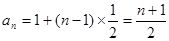 ;(Ⅱ)
;(Ⅱ)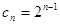 ;(Ⅲ)
;(Ⅲ)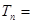
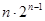 .
.
解析試題分析:(Ⅰ)由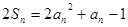 ①
①
得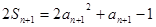 ② 1分
② 1分
由②—①,得 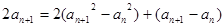
即: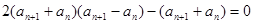 2分
2分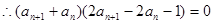 由于數列
由于數列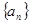 各項均為正數,
各項均為正數,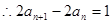 3分
3分
即 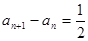
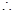 數列
數列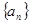 是首項為
是首項為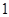 ,公差為
,公差為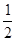 的等差數列,
的等差數列,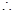 數列
數列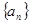 的通項公式是
的通項公式是 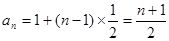 4分
4分
(Ⅱ)由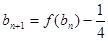 知
知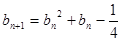 ,
,
所以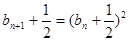 , 5分
, 5分
有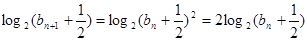 ,即
,即 , 6分
, 6分
而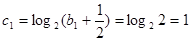 ,
,
故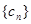 是以
是以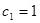 為首項,公比為2的等比數列. 7分
為首項,公比為2的等比數列. 7分
所以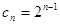 8分
8分
(Ⅲ)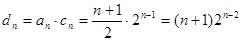 , 9分
, 9分
所以數列 的前n項和
的前n項和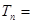
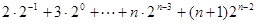
錯位相減可得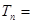
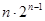 12分
12分
考點:等差數列、等比數列的通項公式, “錯位相減法”。
點評:中檔題,確定數列通項公式,往往利用已知條件,建立相關“元素”的方程組,達到解題目的。 本題利用前n項和與提醒的關系,確定數列的通項公式,也是較為常見的題型。“分組求和法”“裂項相消法”“錯位相減法”是高考常常考查的數列求和方法。本題對運算能力要求較高。


 新課標階梯閱讀訓練系列答案
新課標階梯閱讀訓練系列答案科目:高中數學 來源: 題型:解答題
已知{an}是由非負整數組成的無窮數列,該數列前n項的最大值記為An,第n項之后各項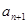 ,
,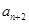 …的最小值記為Bn,dn=An-Bn.
…的最小值記為Bn,dn=An-Bn.
(I)若{an}為2,1,4,3,2,1,4,3…,是一個周期為4的數列(即對任意n∈N*,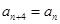 ),寫出d1,d2,d3,d4的值;
),寫出d1,d2,d3,d4的值;
(II)設d為非負整數,證明:dn=-d(n=1,2,3…)的充分必要條件為{an}為公差為d的等差數列;
(III)證明:若a1=2,dn=1(n=1,2,3…),則{an}的項只能是1或2,且有無窮多項為1.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com