
(本題滿分16分)對于數列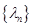 ,若存在常數M>0,對任意
,若存在常數M>0,對任意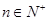 ,恒有
,恒有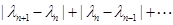
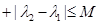 ,則稱數列
,則稱數列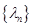 為
為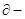 數列.
數列.
求證:⑴設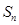 是數列
是數列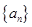 的前n項和,若
的前n項和,若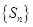 是
是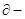 數列,則
數列,則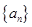 也是
也是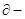 數列.
數列.
⑵若數列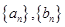 都是
都是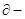 數列,則
數列,則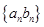 也是
也是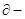 數列.
數列.
科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源:2011屆江西省六校高三聯考數學理卷 題型:解答題
(本題滿分12分)
對甲、乙兩種商品的重量的誤差進行抽查,測得數據如下(單位: ):
):
甲:13 15 14 14 9 14 21 9 10 11
乙:10 14 9 12 15 14 11 19 22 16
(1)畫出樣本數據的莖葉圖,并指出甲,乙兩種商品重量誤差的中位數;
(2)計算甲種商品重量誤差的樣本方差;
(3)現從重量誤差不低于15的乙種商品中隨機抽取兩件,求重量誤差為19的商品被抽
中的概率。
查看答案和解析>>
科目:高中數學 來源:2012-2013學年江蘇省如東縣高三12月四校聯考文科數學試卷(解析版) 題型:解答題
(本題滿分16分)
如圖,開發商欲對邊長為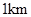 的正方形
的正方形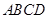 地段進行市場開發,擬在該地段的一角建設一個景觀,需要建一條道路
地段進行市場開發,擬在該地段的一角建設一個景觀,需要建一條道路 (點
(點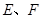 分別在
分別在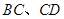 上),根據規劃要求
上),根據規劃要求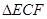 的周長為
的周長為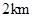 .
.

(1)設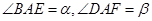 ,求證:
,求證: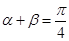 ;
;
(2)欲使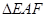 的面積最小,試確定點
的面積最小,試確定點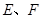 的位置.
的位置.
查看答案和解析>>
科目:高中數學 來源:2011-2012學年上海市楊浦區高三上學期期末學科測試理科數學 題型:解答題
(本題滿分16分)本題共有3個小題,第1小題滿分3分,第2小題滿分6分,第3小
題滿分7分.
已知函數 ,數列
,數列 滿足
滿足 ,
, ,
,
(1). 求 ,
, ,
, 的值;
的值;
(2). 求證:數列 是等差數列;
是等差數列;
(3). 設數列 滿足
滿足 ,
, ,
,
若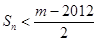 對一切
對一切 成立,求最小正整數
成立,求最小正整數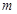 的值.
的值.
查看答案和解析>>
科目:高中數學 來源:2010-2011年江蘇省淮安市高一上學期期末考試數學試卷 題型:解答題
(本題滿分16分)
圍建一個面積為360m2的矩形場地,要求矩形場地的一面利用舊墻(利用的舊墻需維修),其他三面圍墻要新建,在舊墻對面的新墻上要留一個寬度為2m的進出口,如圖所示已知舊墻的維修費用為45元/m,新墻的造價為180元/m,設利用的舊墻長度為x(單位:m),修建此矩形場地圍墻的總費用為y(單位:元)
⑴將y表示為x的函數;
⑵寫出f(x)的單調區間,并證明;
⑶根據⑵,試確定x,使修建此矩形場地圍墻的總費用最小,并求出最小總費用。

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com