
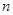 個圖形中有
個圖形中有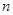 個正三角形中所有小正三角形邊上黑點的總數為
個正三角形中所有小正三角形邊上黑點的總數為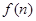 .
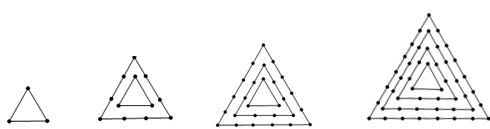
.
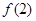 ,
,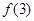 ,
,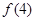 ,
, ;
;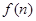 與
與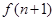 的關系,并求出
的關系,并求出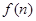 的表達式;
的表達式;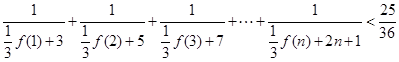 (
(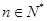 ).
).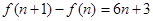 ,
, 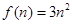 .(Ⅲ)詳見解析.
.(Ⅲ)詳見解析.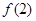 ,
,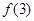 ,
,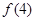 ,
, ,第二個圖形的黑點個數為第一個圖形的黑點個數加上外面的三角形上的黑點個數,即
,第二個圖形的黑點個數為第一個圖形的黑點個數加上外面的三角形上的黑點個數,即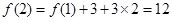 ,第三個圖形的黑點個數為第二個圖形的黑點個數加上外面的三角形上的黑點個數,即
,第三個圖形的黑點個數為第二個圖形的黑點個數加上外面的三角形上的黑點個數,即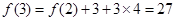 ,以此類推可求出
,以此類推可求出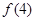 ,
, ;(Ⅱ)觀察
;(Ⅱ)觀察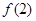 ,
,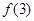 ,
,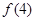 ,
, 可得到,后一個圖形的黑點個數是前一個圖形外多加一個三角形,而且每一條邊都比內一個三角形多兩個黑點,即
可得到,后一個圖形的黑點個數是前一個圖形外多加一個三角形,而且每一條邊都比內一個三角形多兩個黑點,即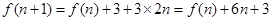 ,即
,即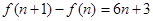 ,求出
,求出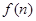 的表達式,像這種關系可用疊加法,即寫出
的表達式,像這種關系可用疊加法,即寫出 ,
,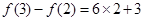 ,
,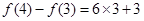 ,
,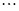 ,
,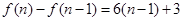 ,把這
,把這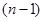 個式子疊加,即可得出
個式子疊加,即可得出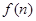 的表達式;(Ⅲ)求證:
的表達式;(Ⅲ)求證: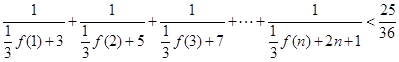 (
(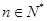 ), 先求出
), 先求出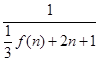 的關系式,得
的關系式,得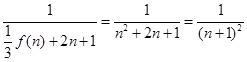 ,由于求證的不等式右邊是常數,可考慮利用放縮法,即
,由于求證的不等式右邊是常數,可考慮利用放縮法,即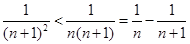 ,這樣既可證明.
,這樣既可證明.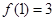 ,
, 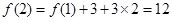 ,
, 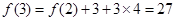 ,
,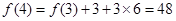 ,
,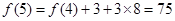 .
.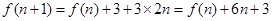 ,
,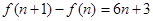 ,所以
,所以 ,
,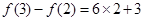 ,
,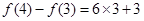 ,
,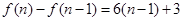 , 5分
, 5分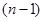 個式子相加,得:
個式子相加,得: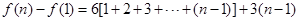
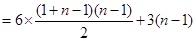
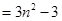 6分
6分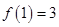 ,所以
,所以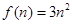 . 7分
. 7分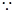
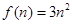 ,∴
,∴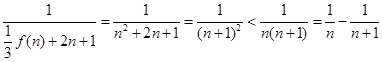 . 9分
. 9分 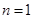 時,
時,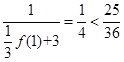 ,原不等式成立. 10分
,原不等式成立. 10分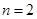 時,
時,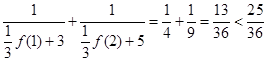 ,原不等式成立. 11分
,原不等式成立. 11分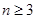 時,
時,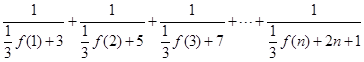
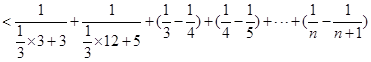
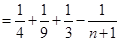
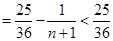 , 原不等式成立. 13分
, 原不等式成立. 13分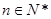 ,原不等式成立. 14分
,原不等式成立. 14分

 100分闖關期末沖刺系列答案
100分闖關期末沖刺系列答案 名校聯盟快樂課堂系列答案
名校聯盟快樂課堂系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com