
 和
和 。假設兩人射擊是否擊中目標,相互之間沒有影響;每次射擊是否擊中目標,相互之間沒有影響。
。假設兩人射擊是否擊中目標,相互之間沒有影響;每次射擊是否擊中目標,相互之間沒有影響。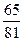 (Ⅱ)
(Ⅱ)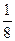 (Ⅲ)
(Ⅲ)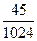
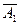 )=1-
)=1-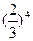 =
=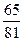 。
。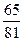 ;……4分
;……4分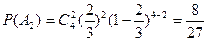 ,
,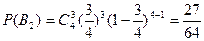 ,
, 。
。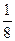 ;…………8分
;…………8分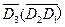 ,且P(Di)=
,且P(Di)=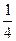 ,由于各事件相互獨立,故P(A3)= P(D5)P(D4)P(
,由于各事件相互獨立,故P(A3)= P(D5)P(D4)P(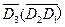 )
)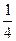 ×
×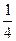 ×
× ×(1-
×(1-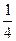 ×
×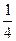 )=
)=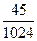 ,
, 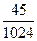 。…………12分
。…………12分

 學習實踐園地系列答案
學習實踐園地系列答案科目:高中數學 來源:不詳 題型:解答題
 .
.查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
 (元)間的每位同學得助學金1500元,家庭收入在
(元)間的每位同學得助學金1500元,家庭收入在 (元)間的每位同學得助學金1000元,家庭收入在
(元)間的每位同學得助學金1000元,家庭收入在 (元),間的同學不發助學金,記該年級某位同學所得助學金為
(元),間的同學不發助學金,記該年級某位同學所得助學金為 元,寫出
元,寫出 的分布列,并計算該企業發放這個年級的助學金約需要的資金;
的分布列,并計算該企業發放這個年級的助學金約需要的資金; 元,求
元,求

查看答案和解析>>
科目:高中數學 來源:不詳 題型:單選題
| A.不全相等 | B.均不相等 |
C.都相等,且為 | D.都相等,且為 |
查看答案和解析>>
科目:高中數學 來源:不詳 題型:單選題
A.
| B.
| C.
| D.
|
查看答案和解析>>
科目:高中數學 來源:不詳 題型:單選題
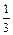 ), Y~B(20,
), Y~B(20, ),那么當X,Y變化時,下面關于P(X=xk)= P(Y=yk)成立的(xk,yk)的個數為( )
),那么當X,Y變化時,下面關于P(X=xk)= P(Y=yk)成立的(xk,yk)的個數為( )| A.10 | B.20 | C.21 | D.0 |
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com