
如圖所示,PA為圓 的切線,A為切點,PBC是過點O的割線,PA=10,PB=5,
的切線,A為切點,PBC是過點O的割線,PA=10,PB=5,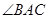 的平分線與BC和圓
的平分線與BC和圓 分別交于點D和E。
分別交于點D和E。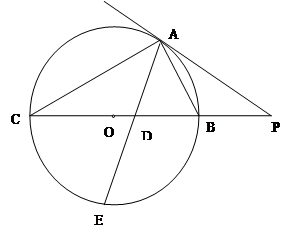
(1)求證: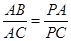 ;
;
(2)求AD·AE的值。
( 1)直接根據∠PAB=∠ACP以及∠P公用,得到△PAB∽△PCA,進而求出結論;
(2)90
解析試題分析:( I)直接根據∠PAB=∠ACP以及∠P公用,得到△PAB∽△PCA,進而求出結論;( II)先根據切割線定理得到PA2=PB•PC;結合第一問的結論以及勾股定理求出 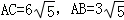 ;再結合條件得到△ACE∽△ADB,進而求出結果.
;再結合條件得到△ACE∽△ADB,進而求出結果.解:( I)∵PA為⊙O的切線,
∴∠PAB=∠ACP,…(1分)
又∠P公用,∴△PAB∽△PCA.…(2分)
∴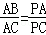 .…(3分)
.…(3分)
( II)∵PA為⊙O的切線,PBC是過點O的割線,
∴PA2=PB•PC.…(5分)
又∵PA=10,PB=5,∴PC=20,BC=15.…(6分)
由( I)知, ,
,
∵BC是⊙O的直徑,
∴∠CAB=90°.
∴AC2+AB2=BC2=225,
∴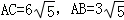 …(7分)
…(7分)
連接CE,則∠ABC=∠E,…(8分)
又∠CAE=∠EAB,
∴△ACE∽△ADB,
∴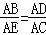 …(9分)
…(9分)
∴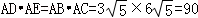 .…(10分)
.…(10分)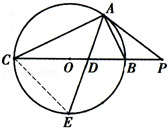
考點:與圓有關的比例線段、相似三角形
點評:本題主要考查與圓有關的比例線段、相似三角形的判定及切線性質的應用.解決本題第一問的關鍵在于先由切線PA得到∠PAB=∠ACP.


 導學教程高中新課標系列答案
導學教程高中新課標系列答案科目:高中數學 來源: 題型:解答題
已知C點在⊙O直徑BE的延長線上,CA切⊙O于A 點,CD是∠ACB的平分線且交AE于點F,交AB于點D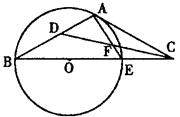
(1)求∠ADF的度數; (2)若AB=AC,求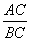 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知,如圖,在平行四邊形ABCD中,延長DA到點E,延長BC到點F,使得AE=CF,連接EF,分別交AB,CD于點M,N,連接DM,BN.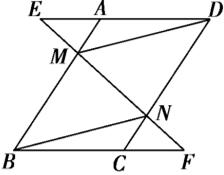
(1)求證:△AEM ≌△CFN;
(2)求證:四邊形BMDN是平行四邊形.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com