
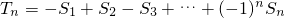 ,求滿足不等式
,求滿足不等式 的所有n的值;
的所有n的值;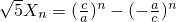 (n∈N+),證明:數列{
(n∈N+),證明:數列{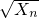 }中的任意連續三項為邊長均可以構成直角三角形,且Xn是正整數.
}中的任意連續三項為邊長均可以構成直角三角形,且Xn是正整數.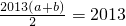 ,即a+b=2.
,即a+b=2.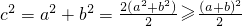 =
=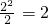 ,
, ;
;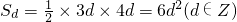 ,則
,則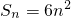 ,
, 得
得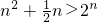 ,
,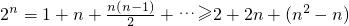 >
>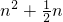 ,
,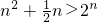 ,當n=1時,
,當n=1時,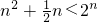 .
. 的所有n的值為2、3、4.
的所有n的值為2、3、4.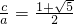 ,
,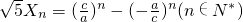 ,得
,得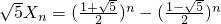 ,
,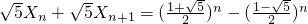
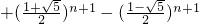
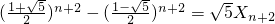 .
.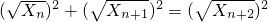 .
.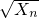 }中的任意連續三項為邊長均可以構成直角三角形.
}中的任意連續三項為邊長均可以構成直角三角形.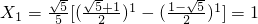 ,
,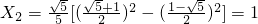 ,
,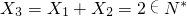 ,
,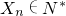 ,
,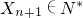 ?Xn+2∈N*,
?Xn+2∈N*, 的所有n的值;
的所有n的值; ,代入
,代入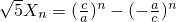 后整理,進一步得到
后整理,進一步得到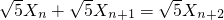 ,由此可證數列{
,由此可證數列{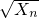 }中的任意連續三項為邊長均可以構成直角三角形,且Xn是正整數.
}中的任意連續三項為邊長均可以構成直角三角形,且Xn是正整數.

 開心練習課課練與單元檢測系列答案
開心練習課課練與單元檢測系列答案科目:高中數學 來源: 題型:
| 5 |
| c |
| a |
| a |
| c |
| Xn |
查看答案和解析>>
科目:高中數學 來源: 題型:
| x2 |
| a2 |
| y2 |
| b2 |
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
| x2 |
| a2 |
| y2 |
| b2 |
查看答案和解析>>
科目:高中數學 來源:2013年廣東省湛江市高考數學二模試卷(文科)(解析版) 題型:解答題
 相交于D、E兩點,△CDE是以C(2,5)為直角頂點的等腰直角三角形,求該橢圓的方程.
相交于D、E兩點,△CDE是以C(2,5)為直角頂點的等腰直角三角形,求該橢圓的方程.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com