
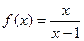
 的圖像關于直線y=x對稱;
的圖像關于直線y=x對稱;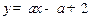 的圖像與函數
的圖像與函數 的圖像有且只有一個交點,求實數
的圖像有且只有一個交點,求實數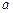 的值;
的值; 的圖象有且只有三個交點,如果存在,則求出此圓的半徑;如果不存在,請說明理由。
的圖象有且只有三個交點,如果存在,則求出此圓的半徑;如果不存在,請說明理由。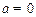 或
或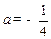 (3)見解析
(3)見解析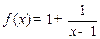 可知函數圖像即為反比例函數
可知函數圖像即為反比例函數 的圖像經向右平移1個單位后再向上平移1個單位得到。則函數圖像關于直線y=x對稱…………………………………….….4’
的圖像經向右平移1個單位后再向上平移1個單位得到。則函數圖像關于直線y=x對稱…………………………………….….4’ 的反函數
的反函數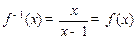 ,所以
,所以 的圖像關于直線y=x對稱………….4’
的圖像關于直線y=x對稱………….4’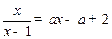 有且只有一解。
有且只有一解。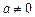 時,由判別式等于0可得
時,由判別式等于0可得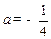 ……………………………………3’
……………………………………3’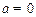 時,由圖像易得同樣滿足題意………………………..………………2’
時,由圖像易得同樣滿足題意………………………..………………2’ 的圖像必在第一象限相切,即圓過(2,2)點,可得圓半徑為
的圖像必在第一象限相切,即圓過(2,2)點,可得圓半徑為 ,所以存在滿足題意的圓,其半徑為
,所以存在滿足題意的圓,其半徑為 ……....4’
……....4’ 代回檢驗得滿足題目要求,所以存在滿足題意的圓,其半徑為
代回檢驗得滿足題目要求,所以存在滿足題意的圓,其半徑為 …..2’
…..2’ 與直線y=x的交點 ……………………………………….……..…..2’
與直線y=x的交點 ……………………………………….……..…..2’ 。r =
。r = 代回檢驗得滿足題目要求,所以存在滿足題意的圓,其半徑為
代回檢驗得滿足題目要求,所以存在滿足題意的圓,其半徑為
 .…………..2’
.…………..2’

科目:高中數學 來源:不詳 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com