Question

若四面體各棱長是1或2，且該四面體不是正四面體，則其體積的值是________．(只須寫出一個可能的值)

Answer 1

答案：
解析：

　　解析：該題的顯著特點是結論發散而不惟一．本題表面上是考查錐體求積公式這個知識點，實際上主要考查由所給條件構造一個四面體的能力，首先得考慮每個面的三條棱是如何構成的．

　　排除{1，1，2}，可得{1，1，1}，{1，2，2}，{2，2，2}，然后由這三類面在空間構造滿足條件的一個四面體，再求其體積．

　　由平時所見的題目，至少可構造出二類滿足條件的四面體，五條邊為2，另一邊為1，對棱相等的四面體．

　　對于五條邊為2，另一邊為1的四面體，參看下圖所示，設AD＝1，取AD的中點為M，平面BCM把三棱錐分成兩個三棱錐，由對稱性可知AD⊥面BCM，且V_A－BCM＝V_D－BCM，所以

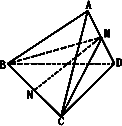
　　V_ABCD＝S_ΔBCM·AD．

　　CM＝＝＝．設N是BC的中點，則MN⊥BC，MN＝＝＝，從而S_ΔBCM＝×2×＝，

　　故V_ABCD＝××1＝．

　　對于對棱相等的四面體，可參見下圖其體積的計算可先將其置于一個長方體之中，再用長方體的體積減去四個小三棱錐的體積來進行．亦可套公式V＝·，

　　不妨令a＝b＝2，c＝1，則

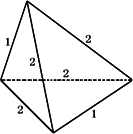
　　V＝·

　　＝·＝．