
 的分布列和數學期望;
的分布列和數學期望;科目:高中數學 來源:不詳 題型:解答題
 . 當
. 當 為何值時, 其發生的概率最大? 說明理由;
為何值時, 其發生的概率最大? 說明理由;  . 求
. 求 的分布列和數學期望.
的分布列和數學期望.查看答案和解析>>
科目:高中數學 來源:不詳 題型:單選題
| A.甲平均擊中的環數比乙平均擊中的環數多 |
| B.乙平均擊中的環數比甲平均擊中的環數多 |
| C.甲、乙兩人平均擊中的環數相等 |
| D.僅依據上述數據,無法判斷誰擊中的環數多 |
查看答案和解析>>
科目:高中數學 來源:不詳 題型:填空題
 ;如果出現一奇一偶,則將它們的差的絕對值記為
;如果出現一奇一偶,則將它們的差的絕對值記為 ,則隨機變量
,則隨機變量 的數學期望為 .
的數學期望為 .查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
 。
。 層樓,寫出
層樓,寫出 的分布列,并求
的分布列,并求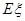 。
。查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
 的
的 個學生,入坐編號為1,2,3,…,
個學生,入坐編號為1,2,3,…, 的
的 個座位.每個學生規定坐一個座位,設學生所坐的座位號與該生的編號不同的學生人數為
個座位.每個學生規定坐一個座位,設學生所坐的座位號與該生的編號不同的學生人數為 ,已知
,已知 時,共有6種坐法.
時,共有6種坐法. 的值;
的值; 的概率分布列和數學期望.
的概率分布列和數學期望.查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
 的所有非空子集中,等可能地取出一個.
的所有非空子集中,等可能地取出一個.  :集合中的所有元素之和為10,求所取出的非空子集滿足性質
:集合中的所有元素之和為10,求所取出的非空子集滿足性質 的概率;
的概率; ,求
,求 的分布列和數學期望
的分布列和數學期望 .
.查看答案和解析>>
科目:高中數學 來源:不詳 題型:單選題
 、
、 、
、 ;已知乙項目的利潤與產品價格的調整有關,在每次調整中價格下降的概率都是
;已知乙項目的利潤與產品價格的調整有關,在每次調整中價格下降的概率都是 ,設乙項目產品價格在一年內進行2次獨立的調整,記乙項目產品價格在一年內的下降次數為
,設乙項目產品價格在一年內進行2次獨立的調整,記乙項目產品價格在一年內的下降次數為 ,對乙項目投資十萬元,
,對乙項目投資十萬元,  取0、1、2時, 一年后相應利潤是1.3萬元、1.25萬元、0.2萬元.隨機變量
取0、1、2時, 一年后相應利潤是1.3萬元、1.25萬元、0.2萬元.隨機變量 、
、 分別表示對甲、乙兩項目各投資十萬元一年后的利潤.
分別表示對甲、乙兩項目各投資十萬元一年后的利潤. 、
、 的概率分布和數學期望
的概率分布和數學期望 、
、 ;
; 時,求
時,求 的取值范圍.
的取值范圍. 查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com