(本小題滿分12分)
求函數(shù)
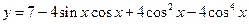
的最大值與最小值。
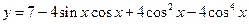
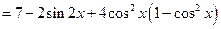
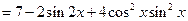
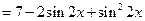
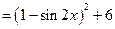
由于函數(shù)
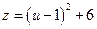
在
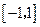
中的最大值為
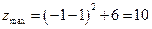
最小值為
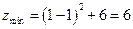
故當
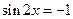
時
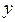
取得最大值
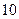
,當
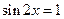
時
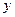
取得最小值
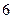
【點評】:此題重點考察三角函數(shù)基本公式的變形,配方法,符合函數(shù)的值域及最值;
【突破】:利用倍角公式降冪,利用配方變?yōu)閺秃虾瘮?shù),重視復合函數(shù)中間變量的范圍是關鍵;
練習冊系列答案
相關習題
科目:高中數(shù)學
來源:不詳
題型:填空題
已知

且α為第二象限角,則m的允許值為
;
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
直線l的傾斜角為θ,
sinθ+cosθ=,則斜率k的值為( )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
已知f(1-cosx)=sin2x,求函數(shù)f(x)的表達式,并求函數(shù)f(x)的值域.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
在△ABC中,a=λ,b=
λ(λ>0),∠A=45°則滿足此條件的三角形有( )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
已知函數(shù)
f(x)=sinωx•cosωx+cos2ωx-(ω>0),直線x=x
1,x=x
2是y=f(x)圖象的任意兩條對稱軸,且|x
1-x
2|的最小值為
.
(I)求f(x)的表達式;
(Ⅱ)將函數(shù)f(x)的圖象向右平移
個單位后,再將得到的圖象上各點的橫坐標伸長為原來的2倍,縱坐標不變,得到函數(shù)y=g(x)的圖象,若關于x的方程g(x)+k=0,在區(qū)間
[0,]上有且只有一個實數(shù)解,求實數(shù)k的取值范圍.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
不等式sin
2x>cos
2x在區(qū)間(0,π)上的解集是
查看答案和解析>>

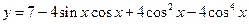 的最大值與最小值。
的最大值與最小值。 中考解讀考點精練系列答案
中考解讀考點精練系列答案