Question

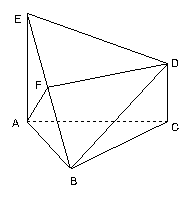
（本題14分）如圖，已知△ABC是正三角形，EA、CD都垂直于平面ABC，且EA＝AB＝2a，DC＝a，F是BE的中點．

（1）FD∥平面ABC；

（2）AF⊥平面EDB．

 

 

 

Answer 1

解析：如圖，已知△ABC是正三角形，EA、CD都垂直于平面ABC，且EA＝AB＝2a，DC＝a，F是BE的中點．

（1）FD∥平面ABC；（2）AF⊥平面EDB．

證明：（1）取AB的中點M，連FM，MC，

∵ F、M分別是BE、BA的中點，

∴ FM∥EA，F(xiàn)M=EA．

∵ EA、CD都垂直于平面ABC，

∴ CD∥EA，∴ CD∥FM．            ………………3分

又 DC=a，∴FM=DC．

∴四邊形FMCD是平行四邊形，

∴ FD∥MC．即FD∥平面ABC．          ……………7分

（2）∵M是AB的中點，△ABC是正三角形，

∴CM⊥AB，又CM⊥AE，

∴CM⊥面EAB，CM⊥AF，F(xiàn)D⊥AF，            ………………………………11分

又F是BE的中點，EA=AB，∴AF⊥EB．

即由AF⊥FD，AF⊥EB，F(xiàn)D∩EB＝F，

可得AF⊥平面EDB．        ……………………………………………………14分