
為加快旅游業的發展,新余市2013年面向國內發行總量為200萬張的“仙女湖之旅”優惠卡,向省外人士發行的是金卡,向省內人士發行的是銀卡.某旅游公司組織了一個有36名游客的旅游團到新余仙女湖旅游,其中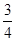 是省外游客,其余是省內游客.在省外游客中有
是省外游客,其余是省內游客.在省外游客中有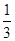 持金卡,在省內游客中有
持金卡,在省內游客中有 持銀卡.(1)在該團中隨機采訪2名游客,求恰有1人持銀卡的概率;
持銀卡.(1)在該團中隨機采訪2名游客,求恰有1人持銀卡的概率;
(2)在該團中隨機采訪2名游客,求其中持金卡與持銀卡人數相等概率.
(1)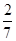 ;(2)
;(2)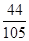 .
.
解析試題分析:(1)根據題意,36人的旅游團中持金卡的人數為: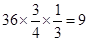 ,
,
持銀卡的人數為: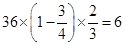 ,可用古典概型求在該團中隨機采訪2名游客,求恰有1人持銀卡的概率;
,可用古典概型求在該團中隨機采訪2名游客,求恰有1人持銀卡的概率;
(2)事件“在該團中隨機采訪2名游客,求其中持金卡與持銀卡人數相等”可看作兩個互斥事件的和事件, 即:“在該團中隨機采訪2名游客,所抽中的兩人都不持有優惠卡”與“在該團中隨機采訪2名游客,所抽中的兩個人中一人持有金卡,另一人持有銀卡”,再用古典概型求這兩個事件的概率即可.
試題解析:(1)由題意得,省外游客有27人,其中9人持金卡;省內游客有9人,其中6人持銀卡.
設事件A為“采訪該團2人,恰有1人持銀卡”, 1分
則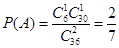
所以采訪該團2人,恰有1人持銀卡的概率是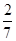 . 6分
. 6分
(2)設事件B為“采訪該團2人,持金卡人數與持銀卡人數相等”,可以分為:
事件B1為“采訪該團2人,持金卡0人,持銀卡0人”,或事件B2為“采訪該團2人,持金卡1人,持銀卡1人”兩種情況,則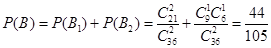
所以采訪該團2人,持金卡與持銀卡人數相等的概率是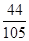 . 12分
. 12分
考點:1、古典概型;2、互斥事件的和事件.


科目:高中數學 來源: 題型:解答題
對于定義域為A的函數f(x),如果任意的x1,x2∈A,當x1<x2時,都有f(x1)<f(x2),則稱函數f(x)是A上的嚴格增函數;函數f(k)是定義在N*上,函數值也在N*中的嚴格增函數,并且滿足條件f(f(k))=3k.
(1)證明:f(3k)=3f(k);
(2)求f(3k-1)(k∈N*)的值;
(3)是否存在p個連續的自然數,使得它們的函數值依次也是連續的自然數;若存在,找出所有的p值,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
設函數f(x)=ax2+bx+b-1(a≠0).
(1)當a=1,b=-2時,求函數f(x)的零點;
(2)若對任意b∈R,函數f(x)恒有兩個不同零點,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某單位擬建一個扇環面形狀的花壇(如圖所示),該扇環面是由以點 為圓心的兩個同心圓弧和延長后通過點
為圓心的兩個同心圓弧和延長后通過點 的兩條直線段圍成.按設計要求扇環面的周長為30米,其中大圓弧所在圓的半徑為10米.設小圓弧所在圓的半徑為
的兩條直線段圍成.按設計要求扇環面的周長為30米,其中大圓弧所在圓的半徑為10米.設小圓弧所在圓的半徑為 米,圓心角為
米,圓心角為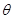 (弧度).
(弧度).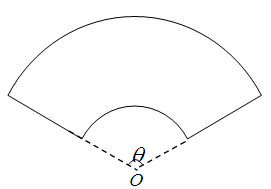
(1)求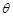 關于
關于 的函數關系式;
的函數關系式;
(2)已知在花壇的邊緣(實線部分)進行裝飾時,直線部分的裝飾費用為4元/米,弧線部分的裝飾費用為9元/米.設花壇的面積與裝飾總費用的比為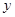 ,求
,求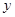 關于
關于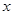 的函數關系式,并求出
的函數關系式,并求出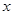 為何值時,
為何值時,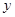 取得最大值?
取得最大值?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知 是正數,
是正數, ,
, ,
, .
.
(Ⅰ)若 成等差數列,比較
成等差數列,比較 與
與 的大小;
的大小;
(Ⅱ)若 ,則
,則 三個數中,哪個數最大,請說明理由;
三個數中,哪個數最大,請說明理由;
(Ⅲ)若 ,
, ,
, (
( ),且
),且 ,
, ,
, 的整數部分分別是
的整數部分分別是

 求所有
求所有 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com