
(本小題11分)如圖,在四棱錐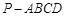 中,
中,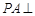 平面
平面 ,
,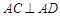 ,
,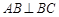 ,
, ,
,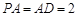 ,
,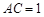 .
.
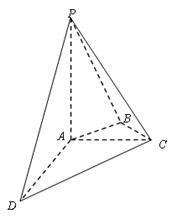
(1)證明: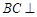 平面
平面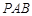
(2)求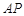 和平面
和平面 所成角的正弦值
所成角的正弦值
(3)求二面角 的正切值;
的正切值;
(1)見解析;(2)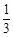 ;(3)
;(3) 。
。
【解析】
試題分析:(1) 平面
平面 ,所以
,所以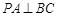 ,又
,又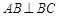
所以 平面
平面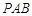 ……………… 2分
……………… 2分
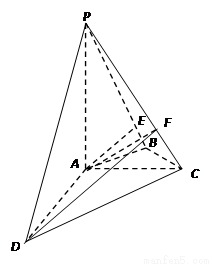
(2)如圖,作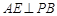 ,交
,交 于點
于點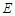 ,
,
 平面
平面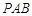 ,
, 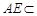 平面
平面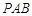 所以
所以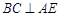
又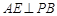 ,所以
,所以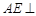 平面
平面
所以 是
是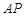 和平面
和平面 所成角………………4分
所成角………………4分
 中,
中,
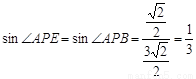 ……………………6分
……………………6分
所以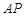 和平面
和平面 所成角的正弦為
所成角的正弦為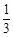 ……………… 7分
……………… 7分
(3)作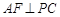 交
交 于點
于點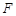 ,連接
,連接
 平面
平面 ,所以
,所以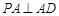 ,又
,又 ,所以
,所以 平面
平面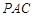 ,所以
,所以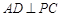
又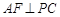 ,所以
,所以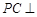 平面
平面 ,所以
,所以 ,
,
所以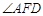 是二面角
是二面角 的平面角。……………… 9分
的平面角。……………… 9分
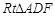 中,
中,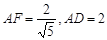 ,
,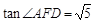
二面角 的正切值為
的正切值為 …………………… 11分
…………………… 11分
(用向量法酌情給分)
考點:線面垂直的性質(zhì)定理;線面垂直的判定定理;面面垂直項性質(zhì)定理;直線與平面所成的角;二面角。
點評:本題主要考查的知識點是二面角的平面角及求法,直線與平面垂直的判定。解決這類問題的常用方法有:綜合法和向量法。本題用的是綜合法,當(dāng)然也可以用向量法。


 名師金手指領(lǐng)銜課時系列答案
名師金手指領(lǐng)銜課時系列答案科目:高中數(shù)學(xué) 來源:2012-2013學(xué)年浙江省高二上期中考試?yán)砜茢?shù)學(xué)試卷(解析版) 題型:解答題
(本小題11分)如圖,三棱錐C—ABD,CB = CD,AB = AD,∠BAD = 90°。E、F分別是BC、AC的中點。
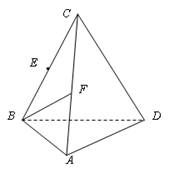
(1)求證:AC⊥BD;
(2)若CA = CB,求證:平面BCD⊥平面ABD
(3)在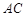 上找一點M,在AD上找點N,使平面MED//平面BFN,說明理由;并求出
上找一點M,在AD上找點N,使平面MED//平面BFN,說明理由;并求出 的值
的值
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
(本小題滿分11分)
 如圖,在ΔOAB中,已知
如圖,在ΔOAB中,已知![]() ,單位圓O與OA交于C,
,單位圓O與OA交于C,![]() ,P為單位圓O上的動點若
,P為單位圓O上的動點若![]() ,求
,求![]() 的值;
的值;
記![]() 的最小值為
的最小值為![]() ,求
,求![]() 的表達式及
的表達式及![]() 的最小值。
的最小值。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
(本小題滿分11分)如圖,在ΔOAB中,已知![]() ,單位圓O與OA交于C,
,單位圓O與OA交于C,![]() ,P為單位圓O上的動點。
,P為單位圓O上的動點。
 (1)若
(1)若![]() ,求
,求![]() 的值;
的值;
(2)若![]() ,求
,求![]() 的值;
的值;
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com