
(07年重慶卷理)(13分)
如圖,在直三棱柱ABC―![]() 中,
中,![]() AB = 1,
AB = 1,![]() ;點D、E分別在
;點D、E分別在![]() 上,且
上,且![]() ,四棱錐
,四棱錐![]() 與直三棱柱的體積之比為3:5。
與直三棱柱的體積之比為3:5。
(1)求異面直線DE與![]() 的距離;(8分)
的距離;(8分)
(2)若BC =![]() ,求二面角
,求二面角![]() 的平面角的正切值。(5分)
的平面角的正切值。(5分)
|
解析:解法一:(Ⅰ)因![]() ,且
,且![]() ,故
,故![]() 面
面![]() ,
,
從而![]() ,又
,又![]() ,故
,故![]() 是異面直線
是異面直線![]() 與
與![]() 的公垂線.
的公垂線.
設![]() 的長度為
的長度為![]() ,則四棱椎
,則四棱椎![]() 的體積
的體積![]() 為
為
![]() .
.
而直三棱柱![]() 的體積
的體積![]() 為
為![]() .
.
由已知條件![]() ,故
,故![]() ,解之得
,解之得![]() .
.
從而![]() .
.
在直角三角形![]() 中,
中,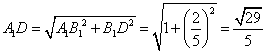 ,
,
又因![]() ,
,
故![]() .
.
(Ⅱ)如答(19)圖1,過![]() 作
作![]() ,垂足為
,垂足為![]() ,連接
,連接![]() ,因
,因![]() ,
,![]() ,故
,故![]() 面
面![]() .
.
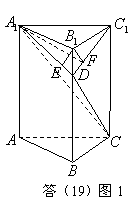
由三垂線定理知![]() ,故
,故![]() 為所求二面角的平面角.
為所求二面角的平面角.
在直角![]() 中,
中,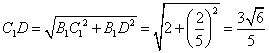 ,
,
又因![]() ,
,
故![]() ,所以
,所以![]() .
.
解法二:
(Ⅰ)如答(19)圖2,以![]() 點為坐標原點
點為坐標原點![]() 建立空間直角坐標系
建立空間直角坐標系![]() ,
,
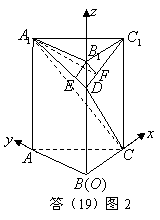
則![]() ,
,![]() ,
,![]() ,
,![]() ,則
,則![]() ,
,![]() .
.
設![]() ,則
,則![]() ,
,
又設![]() ,則
,則![]() ,
,
從而![]() ,即
,即![]() .
.
又![]() ,所以
,所以![]() 是異面直線
是異面直線![]() 與
與![]() 的公垂線.
的公垂線.
下面求點![]() 的坐標.
的坐標.
設![]() ,則
,則![]() .
.
因四棱錐![]() 的體積
的體積![]() 為
為
![]()
![]() .
.
而直三棱柱![]() 的體積
的體積![]() 為
為![]() .
.
由已知條件![]() ,故
,故![]() ,解得
,解得![]() ,即
,即![]() .
.
從而![]() ,
,![]() ,
,![]() .
.
接下來再求點![]() 的坐標.
的坐標.
由![]() ,有
,有![]() ,即
,即![]() (1)
(1)
又由![]() 得
得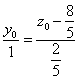 . (2)
. (2)
聯立(1),(2),解得![]() ,
,![]() ,即
,即![]() ,得
,得![]() .
.
故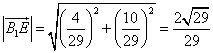 .
.
(Ⅱ)由已知![]() ,則
,則![]() ,從而
,從而![]() ,過
,過![]() 作
作![]() ,
,
垂足為![]() ,連接
,連接![]() ,
,
設![]() ,則
,則![]() ,因為
,因為![]() ,故
,故
![]() ……………………………………①
……………………………………①
因![]() 且
且![]() 得
得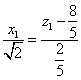 ,即
,即
![]() ……………………………………②
……………………………………②
聯立①②解得![]() ,
,![]() ,即
,即![]() .
.
則![]() ,
,![]() .
.
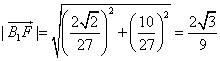 .
.
又![]() ,故
,故![]() ,
,
因此![]() 為所求二面角的平面角.又
為所求二面角的平面角.又![]() ,從而
,從而![]() ,
,
故![]()
![]() ,
,![]() 為直角三角形,所以
為直角三角形,所以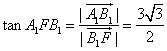 .
.


湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com