
某港口O要將一件重要物品用小艇送到一艘正在航行的輪船上,在小艇出發時,輪船位于港口O北偏西30°且與該港口相距20海里的A處,并正以30海里/小時的航行速度沿正東方向勻速行駛,經過t小時與輪船相遇。
(Ⅰ)若希望相遇時小艇的航行距離最小,則小艇航行速度的大小應為多少?
(Ⅱ)假設小艇的最高航行速度只能達到30海里/小時,試設計航行方案(即確定航行方向和航行速度的大小),使得小艇能以最短時間與輪船相遇,并說明理由。
(Ⅰ)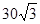 海里/小時(Ⅱ)方案如下:航行方向為北偏東
海里/小時(Ⅱ)方案如下:航行方向為北偏東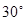 ,航行速度為30海里/小時,小艇能以最短時間與輪船相遇.
,航行速度為30海里/小時,小艇能以最短時間與輪船相遇.
解析試題分析:(I)設相遇時小艇航行的距離為S海里,則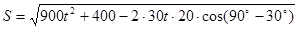
=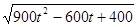
=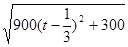 ,
,
故當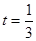 時,
時,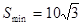 ,此時
,此時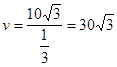 ,
,
即小艇以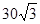 海里/小時的速度航行,相遇時小艇的航行距離最小。
海里/小時的速度航行,相遇時小艇的航行距離最小。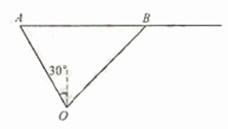
(II)設小艇與輪船在B出相遇,則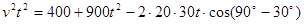 ,
,
故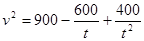 ,
,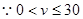 ,
,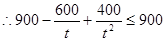 ,
,
即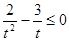 ,解得
,解得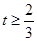 ,
,
又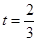 時,
時,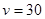 ,
,
故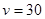 時,t取最小值,且最小值等于
時,t取最小值,且最小值等于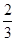 ,
,
此時,在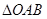 中,有
中,有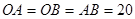 ,故可設計方案如下:
,故可設計方案如下:
航行方向為北偏東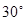 ,航行速度為30海里/小時,小艇能以最短時間與輪船相遇.
,航行速度為30海里/小時,小艇能以最短時間與輪船相遇.
考點:本小題主要考查解三角形在實際問題中的應用.
點評:正弦定理和余弦定理在解三角形中應用十分廣泛,要準確靈活應用,應用正弦定理時要注意解的個數問題.


 全能測控一本好卷系列答案
全能測控一本好卷系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com