必要不充分
分析:作出集合A中不等式組表示的平面區域△ABC和集合B中不等式表示的平面區域圓M及其內部.通過計算點到直線的距離,得到圓M上所有的點落在△ABC的內部或邊界上,由此得到“點P(x,y)∈A”是“點P(x,y)∈B”的必要不充分條件.
解答:如圖所示,集合A中不等式組表示的平面區域為△ABC,
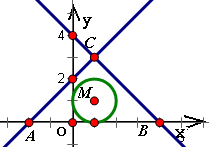
而集合B表示以M(1,1)為圓心、半徑為1的圓及其內部.
∵點M到直線x=0的距離等于1,
點M到直線x+y-4=0的距離等于

,
點M到直線x-y+2=0的距離等于

,
這些距離都大于或等于圓M的半徑
∴△ABC的三條邊中,一條邊與圓M相切,另兩條邊與圓M相離.
由此可得圓M在△ABC的內部.
因此“點P(x,y)∈A”成立不能推出“點P(x,y)∈B”成立,
反之,“點P(x,y)∈B”成立可以推出“點P(x,y)∈A”成立.
∴“點P(x,y)∈A”是“點P(x,y)∈B”的必要不充分
故答案為:必要不充分
點評:本題給出二元一次不等式組表示的平面區域和圓的圖形,叫我們判斷充分必要條件,著重考查了不等式和不等式組表示的平面區域的概念,考查了對充要條件的認識,屬于基礎題.

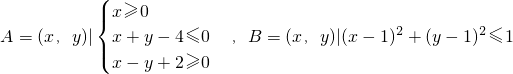 ,則點P(x,y)∈A是點P(x,y)∈B的________條件.
,則點P(x,y)∈A是點P(x,y)∈B的________條件.
 ,
, ,
,
