
設函數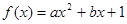 (
(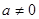 、
、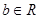 ),若
),若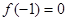 ,且對任意實數
,且對任意實數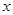 (
(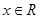 )不等式
)不等式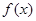
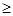 0恒成立.
0恒成立.
(Ⅰ)求實數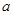 、
、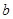 的值;
的值;
(Ⅱ)當 [-2,2]時,
[-2,2]時,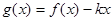 是單調函數,求實數
是單調函數,求實數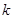 的取值范圍.
的取值范圍.
科目:高中數學 來源: 題型:解答題
(本小題12分)
某市居民生活用水收費標準如下:
用水量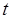 (噸) (噸) | 每噸收費標準(元) |
不超過 噸部分 噸部分 | 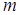 |
超過 噸不超過 噸不超過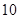 噸部分 噸部分 | 3 |
超過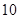 噸部分 噸部分 | 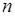 |
 噸,繳納的水費為
噸,繳納的水費為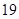 元;二月份用水量為
元;二月份用水量為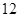 噸,繳納的水費為
噸,繳納的水費為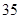 元.設某用戶月用水量為
元.設某用戶月用水量為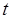 噸,交納的水費為
噸,交納的水費為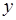 元.
元.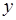 關于
關于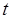 的函數關系式;
的函數關系式;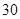 元,求該用戶三月份最多可以用多少噸水?
元,求該用戶三月份最多可以用多少噸水?查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分12分)某單位決定投資3 200元建一倉庫(長方體狀),高度恒定,它的后墻利用舊墻不花錢,正面用鐵柵,每米長造價40元,兩側墻砌磚,每米造價45元,屋頂每平方米造價20元,試計算:
(1)倉庫面積S的最大允許值是多少?
(2)為使S達到最大,而實際投資又不超過預算,那么正面鐵柵應設計為多長?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com