解(Ⅰ)①∵

,∴

∵xf′(x)>f(x),∴g′(x)>0在(0,+∞)上恒成立,
從而有

在(0,+∞)上是增函數.
②由①知

在(0,+∞)上是增函數,當x
1>0,x
2>0時,有

,
于是有:

,
兩式相加得:f(x
1)+f(x
2)<f(x
1+x
2)
(Ⅱ)由(Ⅰ)②可知:f(x
1)+f(x
2)<f(x
1+x
2),(x
1>0,x
2>0)恒成立
由數學歸納法可知:x
i>0(i=1,2,3,…,n)時,有:f(x
1)+f(x
2)+f(x
3)+…+f(x
n)<f(x
1+x
2+x
3+…x
n)(n≥2)恒成立
設f(x)=xlnx,則,則x
i>0(i=1,2,3,…,n)時,x
1lnx
1+x
2lnx
2+…+x
nlnx
n<(x
1+x
2+…+x
n)ln(x
1+x
2+…+x
n)(n≥2)(*)恒成立
令
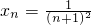
,記

又

,
又
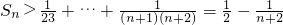
,且ln(x+1)<x
∴(x
1+x
2+…+x
n)ln(x
1+x
2+…+x
n)<(x
1+x
2+…+x
n)ln(1-

)<-

(x
1+x
2+…+x
n)<-

(

-

)=-

(**)
將(**)代入(*)中,可知:-(
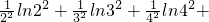

)

于是
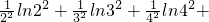

分析:(I)①先利用導數的四則運算,求函數g(x)的導函數,結合已知證明導函數g′(x)>0在(0,+∞)上恒成立,即可證明其在(0,+∞)上是增函數;②利用①的結論,且x
1>0,x
2>0時,x
1+x
2>x
1,且x
1+x
2>x
2,得

,從中解出f(x
1)、f(x
2)即可證得結論;(II)構造一個符合條件的函數f(x)=xlnx,利用(I)的結論,得x
1lnx
1+x
2lnx
2+…+x
nlnx
n<(x
1+x
2+…+x
n)ln(x
1+x
2+…+x
n)(n≥2),令
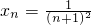
,再將

放縮,即可證得所證不等式
點評:本題綜合考查了導數的四則運算,利用導數證明函數的單調性,利用函數的單調性證明不等式,以及利用函數性質構造數列證明數列不等式的方法,難度較大

 在(0,+∞)上是增函數;
在(0,+∞)上是增函數;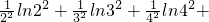 …
…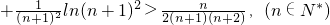 .
. ,∴
,∴
 在(0,+∞)上是增函數.
在(0,+∞)上是增函數. 在(0,+∞)上是增函數,當x1>0,x2>0時,有
在(0,+∞)上是增函數,當x1>0,x2>0時,有 ,
, ,
,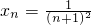 ,記
,記
 ,
,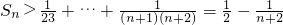 ,且ln(x+1)<x
,且ln(x+1)<x )<-
)<- (x1+x2+…+xn)<-
(x1+x2+…+xn)<- (
( -
- )=-
)=- (**)
(**)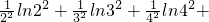
 )
)
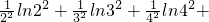

 ,從中解出f(x1)、f(x2)即可證得結論;(II)構造一個符合條件的函數f(x)=xlnx,利用(I)的結論,得x1lnx1+x2lnx2+…+xnlnxn<(x1+x2+…+xn)ln(x1+x2+…+xn)(n≥2),令
,從中解出f(x1)、f(x2)即可證得結論;(II)構造一個符合條件的函數f(x)=xlnx,利用(I)的結論,得x1lnx1+x2lnx2+…+xnlnxn<(x1+x2+…+xn)ln(x1+x2+…+xn)(n≥2),令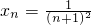 ,再將
,再將 放縮,即可證得所證不等式
放縮,即可證得所證不等式

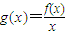 在(0,+∞)上是增函數;
在(0,+∞)上是增函數;