【答案】
分析:(1)由題意知本題是一個等可能事件的概率,試驗發生所包含的事件數通過分類列舉共有24種結果,滿足條件的事件列舉出共有6種結果,根據等可能事件的概率公式得到結果.
(2)由題意知本題是一個等可能事件的概率,試驗發生所包含的事件數通過第一問列舉得到共有24種結果,滿足條件的事件數也可以通過列舉得到,最后求得概率.
解答:解:(1)由題意知本題是一個等可能事件的概率,
試驗發生所包含的事件數通過列舉得到
A排第一的情況:(A,B,C,D),(A,B,D,C),(A,C,B,D),(A,C,D,B)
(A,D,B,C),(A,D,C,B)
B排第一的情況:(B,A,C,D),(B,A,D,C),(B,C,A,D),(B,C,D,A)
(B,D,A,C),(B,D,C,A)
C排第一的情況:(C,A,B,D),(C,A,D,B),(C,,B,A,D),(C,B,D,A)
(C,D,A,B),(C,D,B,A)
D排第一的情況:(D,A,B,C),(D,A,C,B),(D,B,A,C),(D,B,C,A)
(D,C,A,B),(D,C,B,A)共24種情況
滿足條件的事件恰好有兩名同學排名不變的是:(A,B,D,C)(A,C,B,D),(A,D,C,B),(D,B,C,A),(C,,B,A,D),(B,A,C,D),共6種情況
所以恰好有兩名同學排名不變的概率為
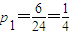
(2)由題意知本題是一個等可能事件的概率,
試驗發生所包含的事件數通過第一問列舉得到共有24種結果
滿足條件的事件是四名同學排名全變的是:(B,A,D,C),(B,C,D,A),(B,D,A,C),
(B,D,C,A),(C,A,D,B),(C,D,A,B),(C,D,B,A),(D,A,B,C),(D,A,C,B)共9種情況
所以四名同學排名全變的概率為
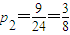 點評:
點評:本題考查等可能事件的概率,本題解題的關鍵是通過分類列舉得到所有的事件數和滿足條件的事件數,在列舉時要按照一定的規律分類,做到不重不漏,本題是一個基礎題.

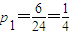
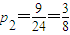


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案