
用數(shù)學(xué)歸納法證明不等式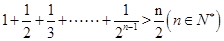 ,第二步由k到k+1時(shí)不等式左邊需增加( )
,第二步由k到k+1時(shí)不等式左邊需增加( )
A.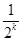 | B.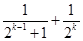 |
C.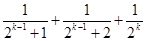 | D.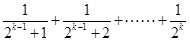 |

| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:單選題
設(shè) 是定義在正整數(shù)集上的函數(shù),且
是定義在正整數(shù)集上的函數(shù),且 滿足:“當(dāng)
滿足:“當(dāng) 成立時(shí),總可推出
成立時(shí),總可推出 成立”,那么,下列命題總成立的是 ( )
成立”,那么,下列命題總成立的是 ( )
A.若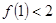 成立,則 成立,則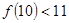 成立 成立 |
B.若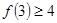 成立,則當(dāng) 成立,則當(dāng)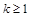 時(shí),均有 時(shí),均有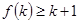 成立 成立 |
C.若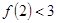 成立,則 成立,則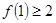 成立 成立 |
D.若 成立,則當(dāng) 成立,則當(dāng) 時(shí),均有 時(shí),均有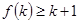 成立 成立 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:單選題
有一段演繹推理是這樣的:“直線平行于平面,則平行于平面內(nèi)所有直線;已知直線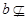 平面
平面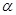 ,直線
,直線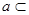 平面
平面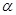 ,直線
,直線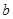 ∥平面
∥平面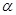 ,則直線
,則直線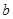 ∥直線
∥直線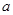 ”的結(jié)論顯然是錯(cuò)誤的,這是因?yàn)?nbsp;( )
”的結(jié)論顯然是錯(cuò)誤的,這是因?yàn)?nbsp;( )
| A.大前提錯(cuò)誤 | B.小前提錯(cuò)誤 | C.推理形式錯(cuò)誤 | D.非以上錯(cuò)誤 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:單選題
用數(shù)學(xué)歸納法證明等式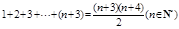 時(shí),第一步驗(yàn)證
時(shí),第一步驗(yàn)證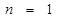 時(shí),左邊應(yīng)取的項(xiàng)是
時(shí),左邊應(yīng)取的項(xiàng)是
| A.1 | B.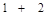 | C. | D.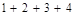 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:單選題
用反證法證明命題:“a,b∈N,ab可被5整除,那么a,b中至少有一個(gè)能被5整除”時(shí),假設(shè)的內(nèi)容應(yīng)為( )
| A.a(chǎn),b都能被5整除 | B.a(chǎn),b都不能被5整除 |
| C.a(chǎn),b不都能被5整除 | D.a(chǎn)不能被5整除 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:單選題
由“半徑為R的圓內(nèi)接矩形中,正方形的面積最大”,推理出“半徑為R的球的內(nèi)接長(zhǎng)方體中,正方體的體積最大”是( )
| A.歸納推理 | B.類比推理 | C.演繹推理 | D.以上都不是 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
如圖的三角形數(shù)陣中,滿足:(1)第1行的數(shù)為1;(2)第 (
( )行首尾兩數(shù)均為
)行首尾兩數(shù)均為 ,其余的數(shù)都等于它肩上的兩個(gè)數(shù)相加,則第
,其余的數(shù)都等于它肩上的兩個(gè)數(shù)相加,則第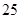 行中第
行中第 個(gè)數(shù)是____________.
個(gè)數(shù)是____________.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
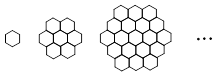
蜜蜂被認(rèn)為是自然界中最杰出的建筑師,單個(gè)蜂巢可以近似地看作是一個(gè)正六邊形,如圖為
一組蜂巢的截面圖.其中第一個(gè)圖有1個(gè)蜂巢,第二個(gè)圖有7個(gè)蜂巢,第三個(gè)圖有19個(gè)蜂巢,
按此規(guī)律,以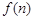 表示第
表示第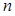 幅圖的蜂巢總數(shù).則
幅圖的蜂巢總數(shù).則 =_____,
=_____, =___________.
=___________.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:單選題
用數(shù)學(xué)歸納法證明“當(dāng)n為正奇數(shù)時(shí),xn+yn能被x+y整除”的第二步
是( ).
| A.假使n=2k+1時(shí)正確,再推n=2k+3正確 |
| B.假使n=2k-1時(shí)正確,再推n=2k+1正確 |
| C.假使n=k時(shí)正確,再推n=k+1正確 |
| D.假使n≤k(k≥1),再推n=k+2時(shí)正確(以上k∈N+) |
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com