
| p | 1-p |
| p |
| 1-p |
| p |
| 1-p |
| an |
| an-1 |
| p |
| 1-p |
| p |
| 1-p |
| p |
| 1-p |
| an |
| an-1 |
|


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
①若p=q=0,則“距離坐標”為(0,0)的點有且僅有1個.
②若pq=0,且p+q≠0,則“距離坐標”為(p,q)的點有且僅有2個.
③若pq≠0,則“距離坐標”為(p,q)的點有且僅有4個.
上述命題中,正確命題的個數是( )
A.0 B.1 C.2 D.3
查看答案和解析>>
科目:高中數學 來源: 題型:

①若p=q=0,則“距離坐標”為(0,0)的點有且僅有1個.
②若pq=0,且p+q≠0,則“距離坐標”為(p,q)的點有且僅有2個.
③若pq≠0,則“距離坐標”為(p,q)的點有且僅有4個.
上述命題中,正確命題的個數是( )
A.0 B.1 C.2 D.3
查看答案和解析>>
科目:高中數學 來源: 題型:
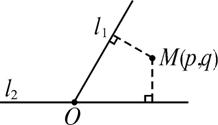
如圖,平面中兩條直線l1和l2相交于點O,對于平面上任意一點M,若p,q分別是M到直線l1和l2的距離,則稱有序非負實數對(p,q)是點M的“距離坐標”,已知常數p≥0,q≥0,給出下列三個命題:

①若p=q=0,則“距離坐標”為(0,0)的點有且僅有1個.
②若pq=0,且p+q≠0,則“距離坐標”為(p,q)的點有且僅有2個.
③若pq≠0,則“距離坐標”為(p,q)的點有且僅有4個.
上述命題中,正確命題的個數是( )
A.0 B.1 C.2 D.3
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
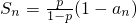 數列{bn}滿足bn+1-bn=logpa2n-1且b1=1,
數列{bn}滿足bn+1-bn=logpa2n-1且b1=1,查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com