
【選修4—4:坐標系與參數方程】
已知圓 的參數方程為
的參數方程為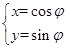 (
(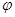 為參數),以坐標原點
為參數),以坐標原點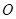 為極點,
為極點,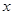 軸的正半軸為極軸建立極坐標系,圓
軸的正半軸為極軸建立極坐標系,圓 的極坐標方程為
的極坐標方程為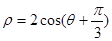 .
.
(I)將圓 的參數方程化為普通方程,將圓
的參數方程化為普通方程,將圓 的極坐標方程化為直角坐標方程;
的極坐標方程化為直角坐標方程;
(II)圓 、
、 是否相交,若相交,請求出公共弦的長;若不相交,請說明理由.
是否相交,若相交,請求出公共弦的長;若不相交,請說明理由.
(I)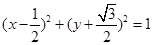 ;(II)|AB|=
;(II)|AB|=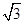
【解析】
試題分析:(I)由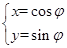 得x2+y2=1,
得x2+y2=1,
又∵ρ=2cos(θ+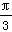 )=cosθ-
)=cosθ-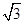 sinθ,
sinθ,
∴ρ2=ρcosθ-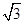 ρsinθ.
ρsinθ.
∴x2+y2-x+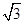 y=0,即
y=0,即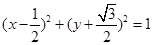
(II)圓心距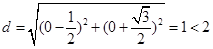 ,得兩圓相交
,得兩圓相交
由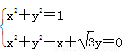 得,A(1,0),B
得,A(1,0),B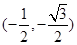 ,
,
∴|AB|=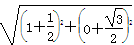 =
=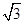
考點:本題主要考查極坐標方程與普通方程的互化,直線與圓的位置關系。
點評:中檔題,學習參數方程、極坐標,其中一項基本的要求是幾種不同形式方程的互化,其次是應用極坐標、參數方程,簡化解題過程。參數方程的應用,往往可以把曲線問題轉化成三角問題,也可在計算弦長時發揮較好作用。本題(II)利用“代數法”求弦長,也可考慮應用“特征直角三角形”,利用勾股定理求弦長。


科目:高中數學 來源: 題型:
| π |
| 3 |
| ||
| sinθ+cosθ |
|
查看答案和解析>>
科目:高中數學 來源: 題型:
|
| 5 |
| 5 |
查看答案和解析>>
科目:高中數學 來源:2011-2012學年云南省高三上學期12月月考理科數學試卷 題型:解答題
【選修4—4:坐標系與參數方程】 以直角坐標系的原點 為極點,
為極點,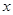 軸的正半軸為極軸,已知點
軸的正半軸為極軸,已知點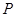 的直角坐標為
的直角坐標為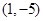 ,點
,點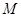 的極坐標為
的極坐標為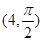 ,若直線
,若直線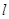 過點
過點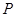 ,且傾斜角為
,且傾斜角為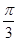 ,圓
,圓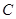 以
以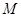 為 圓心、
為 圓心、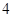 為半徑。
為半徑。
(I) 寫出直線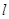 的參數方程和圓
的參數方程和圓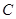 的極坐標方程;
的極坐標方程;
(Ⅱ)試判定直線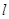 和圓
和圓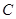 的位置關系。
的位置關系。
查看答案和解析>>
科目:高中數學 來源: 題型:
【選修4—4:坐標系與參數方程】
以直角坐標系的原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸建立極坐標系,已知點
軸的正半軸為極軸建立極坐標系,已知點![]() 的直角坐標為
的直角坐標為![]() ,點
,點![]() 的極坐標為
的極坐標為![]() ,若直線
,若直線![]() 過點
過點![]() ,且傾斜角為
,且傾斜角為![]() ,圓
,圓![]() 以點
以點![]() 為 圓心、
為 圓心、![]() 為半徑。
為半徑。
(Ⅰ)寫出直線![]() 的參數方程和圓
的參數方程和圓![]() 的極坐標方程;
的極坐標方程;
(Ⅱ)試判定直線![]() 和圓
和圓![]() 的位置關系。
的位置關系。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com