(本題9分)設函數(shù)
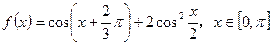
。
(1)求
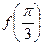
的值;
(2)求

的最小值及

取最小值時
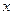
的集合;(3)求

的單調(diào)遞增區(qū)間。
解:(1)
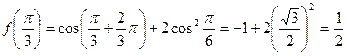
。………3分
(2)
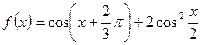
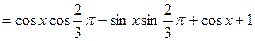
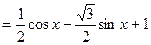
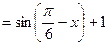
。
因為
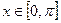
,所以
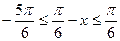
,所以
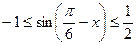
。
所以函數(shù)

的最小值為0。
此時
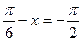
,即
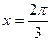
。所以
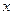
的取值集合為
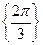
。

……………6分
(3)由(2)可知:
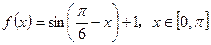
。
設
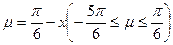
,則原函數(shù)為
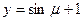
。
因為
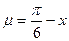
為減函數(shù),所以
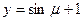
的減區(qū)間就是復合函數(shù)

的增區(qū)間。
由
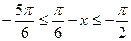
,得
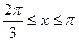
。
所以,函數(shù)

的單調(diào)遞增區(qū)間是
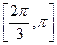
。………………………………………9分
練習冊系列答案
相關習題
科目:高中數(shù)學
來源:不詳
題型:填空題
若函數(shù)f(x)在定義域R內(nèi)可導,f(2+x)=f(2-x),且當x∈(-∞

,2)時,(x-2)
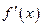
>0.設a=f(1

),
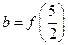
,c=f(4),則a,b,c的大小為
.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
(本小題滿分14分)
已知函數(shù)
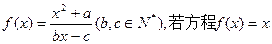
有且只有兩個相異實根0,2,且
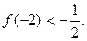
(Ⅰ)求函數(shù)
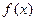
的解析式;
(Ⅱ)已知各項均不為1的數(shù)列
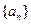
滿足
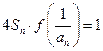
,求通
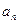
,
(Ⅲ)設
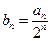
,求數(shù)列
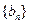
的前
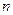
項和
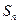
.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
設函數(shù)
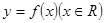
是可導的函數(shù),若滿足
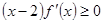
,則必有
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
定義在R上的可導函數(shù)f(x),已知
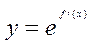
的圖象如下圖所示,
則y=f(x)的增區(qū)間是( )
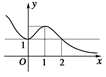
| A.(-∞,1) | B.(0,1) |
| C.(-∞,2) | D.(1,2) |
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
(本小題滿分12分)
用長為18 cm的鋼條圍成一個長方體形狀的框架,要求長方體的長與寬之比為2:1,問該長

方體的長、寬、高各為多少時,其體積最大?最大體積是多少?
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
(本小題滿分12分)已知f(x)=ex-ax-1.
(1)求f(x)的單調(diào)增區(qū)間;
(2)若f(x)在定義域R內(nèi)單調(diào)遞增,求a的取值范圍;
(3)是否存在a,使f(x)在(-∞,0]上單調(diào)遞減,在[0,+∞)上單調(diào)遞增?若存在,求出a的值;若不存在,說明理由.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
已知函數(shù)
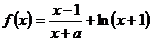
,其中實數(shù)
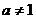
。
(1)若
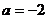
,求曲線
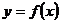
在點
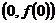
處的切線方程;
(2)若
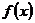
在
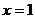
處取得極值,試討論
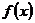
的單調(diào)性。
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
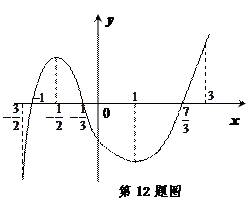
已知函數(shù)
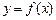
的定義域為
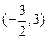
,且
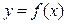
的圖像如右圖所示,記
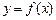
的導函數(shù)為
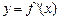
,則不等式
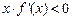
的解集是
▲ .
查看答案和解析>>

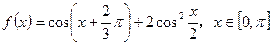 。
。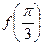 的值;
的值; 的最小值及
的最小值及 取最小值時
取最小值時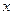 的集合;(3)求
的集合;(3)求 的單調(diào)遞增區(qū)間。
的單調(diào)遞增區(qū)間。 ,2)時,(x-2)
,2)時,(x-2)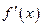 >0.設a=f(1
>0.設a=f(1 ),
),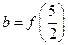 ,c=f(4),則a,b,c的大小為 .
,c=f(4),則a,b,c的大小為 .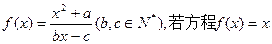 有且只有兩個相異實根0,2,且
有且只有兩個相異實根0,2,且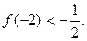
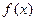 的解析式;
的解析式; 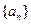 滿足
滿足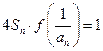 ,求通
,求通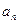 ,
,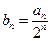 ,求數(shù)列
,求數(shù)列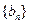 的前
的前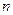 項和
項和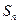 .
.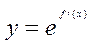 的圖象如下圖所示,
的圖象如下圖所示,
 方體的長、寬、高各為多少時,其體積最大?最大體積是多少?
方體的長、寬、高各為多少時,其體積最大?最大體積是多少?