Question

已知橢圓的方程為=1(a＞b＞0),過其左焦點F(-1,0)、斜率為1的直線交橢圓于P、Q兩點.

(1)若與a=(-3,1)共線,求橢圓的方程;

(2)若在左準線上存在點R,使△PQR為正三角形,求橢圓的離心率e.

(文)已知函數f(x)=2x(x＞0),g(x)=.

(1)求F(x)=2f(x)+［g(x)］²的最小值;

(2)在x軸正半軸上有一動點C(x,0),過C作x軸的垂線分別與f(x)、g(x)的圖象交于點A、B,試將△AOC與△BOC的面積的平方差表示為x的函數h(x),并判斷h(x)是否存在極值,若存在,求出極值;若不存在,請說明理由.

Answer 1

答案：解:(1)將直線PQ的方程y=x+1,代入+=1并化簡,得(a²+b²)x²+2a²x+a²-a²b²=0.

令P(x₁,y₁),Q(x₂,y₂),則x₁+x₂=,x₁x₂=.

由=(x₁+x₂,y₁+y₂),與a=(-3,1)共線,得3(y₁+y₂)+(x₁+x₂)=0.

∴3(x₁+x₂+2)+(x₁+x₂)=0.∴x₁+x₂=-,即=-.∴a²=3b².

又a²=b²+1,∴a²=,b²=.∴橢圓的方程為+2y²=1.

(2)如圖,設線段PQ的中點為M.

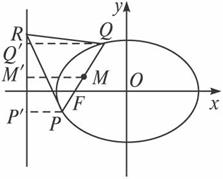
過點P、M、Q分別作準線的垂線,垂足分別為P′、M′、Q′,則|MM′|=(|PP′|+|QQ′|)

=.∵∠QFX=,∴∠FMM′=.∴∠M′MR=.∴|RM|=|MM′|.又|RM|=|PQ|,∴|PQ|.∴e=.

(文)解：(1)F(x)=2x+≥2,當且僅當2x=,即x=時取等號.

(2)△AOC與△BOC的面積分別為x²、,所以h(x)=(2x⁴-x),h′(x)=(8x³-1).

當0＜x＜時,h′(x)＜0,h(x)在(0,)上單調遞減;當x＞時,h′(x)＞0,h(x)在(,+∞)上單調遞增,且h(x)在(0,+∞)上連續,所以h(x)在x=處有極小值h()=.