
如圖,三棱柱ABC-A1B1C1的所有棱長都是2,又AA1⊥平面ABC,D,E分別是AC,CC1的中點.

(1)求證:AE⊥平面A1BD.
(2)求二面角D-BA1-A的余弦值.
(3)求點B1到平面A1BD的距離.
(1)見解析 (2) 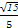 (3)
(3) 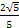
【解析】由AA1⊥平面ABC可知,平面ABC⊥平面ACC1A1,故可考慮建立空間直角坐標系解決問題.
【解析】
(1)以D為原點,DA所在直線為x軸,過D作AC的垂線為y軸,DB所在直線為z軸建立空間直角坐標系如圖,
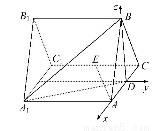
則A(1,0,0),C(-1,0,0),E(-1,-1,0),A1(1,-2,0),C1(-1,-2,0),B(0,0,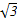 ),B1(0,-2,
),B1(0,-2,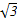 ),
),
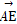 =(-2,-1,0),
=(-2,-1,0),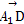 =(-1,2,0),
=(-1,2,0),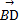 =(0,0,-
=(0,0,-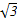 ).∴
).∴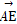 ·
·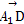 =2-2+0=0,
=2-2+0=0,
∴AE⊥A1D,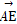 ·
·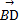 =0,∴AE⊥BD.
=0,∴AE⊥BD.
又A1D與BD相交于D,∴AE⊥平面A1BD.
(2)設平面DA1B的一個法向量為n1=(x1,y1,z1),
由 ⇒
⇒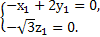 取n1=(2,1,0).
取n1=(2,1,0).
設平面AA1B的一個法向量為n2=(x2,y2,z2),
易得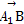 =(-1,2,
=(-1,2,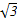 ),
),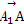 =(0,2,0),
=(0,2,0),
則由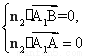 ⇒
⇒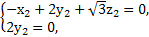
取n2=(3,0,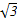 ).cos<n1,n2>=
).cos<n1,n2>=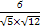 =
=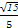 .
.
故二面角D-BA1-A的余弦值為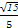 .
.
(3)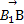 =(0,2,0),平面A1BD的法向量取n1=(2,1,0),則點B1到平面A1BD的距離為d=|
=(0,2,0),平面A1BD的法向量取n1=(2,1,0),則點B1到平面A1BD的距離為d=|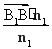 |=
|=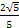 .
.


 智能訓練練測考系列答案
智能訓練練測考系列答案 計算高手系列答案
計算高手系列答案科目:高中數學 來源:2014年高考數學全程總復習課時提升作業四十四第七章第三節練習卷(解析版) 題型:選擇題
如圖,正三棱柱ABC-A1B1C1的各棱長(包括底面邊長)都是2,E,F分別是AB,A1C1的中點,則EF與側棱C1C所成的角的余弦值是( )
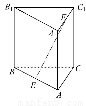
(A)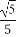 (B)
(B)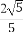 (C)
(C) (D)2
(D)2
查看答案和解析>>
科目:高中數學 來源:2014年高考數學全程總復習課時提升作業四十五第七章第四節練習卷(解析版) 題型:解答題
如圖所示,在棱長為1的正方體ABCD-A1B1C1D1中,點M在AD1上移動,點N在BD上移動,D1M=DN=a(0<a<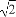 ),連接MN.
),連接MN.
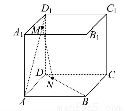
(1)證明對任意a∈(0,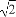 ),總有MN∥平面DCC1D1.
),總有MN∥平面DCC1D1.
(2)當a為何值時,MN的長最小?
查看答案和解析>>
科目:高中數學 來源:2014年高考數學全程總復習課時提升作業四十二第七章第一節練習卷(解析版) 題型:解答題
已知正三棱錐V-ABC的正視圖、側視圖和俯視圖如圖所示.
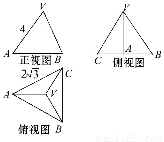
(1)畫出該三棱錐的直觀圖.
(2)求出側視圖的面積.
查看答案和解析>>
科目:高中數學 來源:2014年高考數學全程總復習課時提升作業四十二第七章第一節練習卷(解析版) 題型:選擇題
如圖,△ABC為正三角形,AA'∥BB'∥CC',CC'⊥平面ABC且3AA'= BB'=CC'=AB,則多面體ABC-A'B'C'的正視圖是( )
BB'=CC'=AB,則多面體ABC-A'B'C'的正視圖是( )
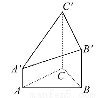
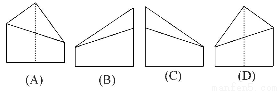
查看答案和解析>>
科目:高中數學 來源:2014年高考數學全程總復習課時提升作業四十九第七章第八節練習卷(解析版) 題型:填空題
如圖,正方體ABCD-A1B1C1D1的棱長為1,O是底面A1B1C1D1的中心,則點O到平面ABC1D1的距離為 .

查看答案和解析>>
科目:高中數學 來源:2014年高考數學全程總復習課時提升作業四十九第七章第八節練習卷(解析版) 題型:選擇題
已知空間三點A(1,1,1),B(-1,0, 4),C(2,-2,3),則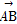 與
與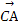 的夾角θ的大小是( )
的夾角θ的大小是( )
(A) (B)
(B) π (C)
π (C) (D)
(D) π
π
查看答案和解析>>
科目:高中數學 來源:2014年高考數學全程總復習課時提升作業四十三第七章第二節練習卷(解析版) 題型:選擇題
如圖是某幾何體的三視圖,其中正視圖和側視圖是半徑為1的半圓,俯視圖是個圓,則該幾何體的全面積是( )
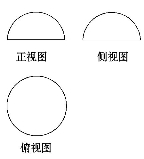
(A)π (B)2π (C)3π (D)4π
查看答案和解析>>
科目:高中數學 來源:2014年高考數學全程總復習課時提升作業四十 第六章第六節練習卷(解析版) 題型:選擇題
已知函數f(x)是R上的單調增函數且為奇函數,數列{an}是等差數列,a3>0,則f(a1)+f(a3)+f(a5)的值( )
(A)恒為正數 (B)恒為負數
(C)恒為0 (D)可正可負
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com