|
|
|
在數列{xn}中,a1=1, ,猜想這個數列的一個通項公式為 ,猜想這個數列的一個通項公式為
|
| [ ] |
A. |
an=n
|
B. |
an=2n-1
|
C. |
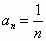
|
D. |
an=n2
|
|
|
練習冊系列答案
相關習題
科目:高中數學
來源:人民教育出版社 代數
題型:
|
|
|
在R上定義運算 :x :x y=x(1-y),要使不等式(x-a) y=x(1-y),要使不等式(x-a) (x+a)>1成立,則實數a的取值范圍是 (x+a)>1成立,則實數a的取值范圍是
|
| [ ] |
A. |
-1<a<1
|
B. |
0<a<2
|
C. |
a<- 或a> 或a>
|
D. |
- <a< <a<
|
|
|
查看答案和解析>>
科目:高中數學
來源:人民教育出版社 代數
題型:
|
|
|
已知函數f(x)=ln(x-1)+ (a∈R). (a∈R).
(1)若a=2時,試證明:當x≥2時,f(x)≥1;
(2)如果函數y=f(x)是定義域上的增函數,求a的取值范圍;
(3)求證:ln(n+1)> + +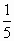 + + +…+ +…+ (n∈N*). (n∈N*).
|
|
|
查看答案和解析>>
科目:高中數學
來源:人民教育出版社(實驗修訂本) 高中數學
題型:
|
|
|
函數f(x)的導函數為 (x),對任意的x∈R都有2 (x),對任意的x∈R都有2 (x)>f(x)成立,則 (x)>f(x)成立,則
|
| [ ] |
A. |
3f(2ln2)>2f(2ln3)
|
B. |
3f(2ln2)<2f(2ln3)
|
C. |
3f(2ln2)=2f(2ln3)
|
D. |
3f(2ln2)與2f(2ln3)的大小不確定
|
|
|
查看答案和解析>>
科目:高中數學
來源:人民教育出版社(實驗修訂本) 高中數學
題型:
|
|
|
已知函數f(x)=2x2-4x+4+xlnx+8 m,m為實數.
(Ⅰ)證明:當x∈[1,+∞)時,f(x)≥(x-1)lnx+x+8 m+1恒成立;
(Ⅱ)當x>2時,f(x)>4 mx恒成立,求整數m的最大值.
|
|
|
查看答案和解析>>
科目:高中數學
來源:人民教育出版社(實驗修訂本) 高中數學
題型:
|
|
|
函數 在x等于________處取得極值. 在x等于________處取得極值.
|
|
|
查看答案和解析>>
科目:高中數學
來源:人民教育出版社(實驗修訂本) 高中數學
題型:
|
|
|
等比數列{an}中,已知對任意正自然數n,a1+a2+a3+…+an=2n-1,則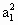 + + + + +…+a +…+a 等于 等于
|
| [ ] |
A. |
(2n-1)2
|
B. |
 (2n-1) (2n-1)
|
C. |
4n-1
|
D. |
 (4n-1) (4n-1)
|
|
|
查看答案和解析>>
科目:高中數學
來源:人教B版(新課標) 選修1-1
題型:
|
|
|
已知雙曲線 的實軸在y軸上且焦距為8,則雙曲線的漸近線的方程為 的實軸在y軸上且焦距為8,則雙曲線的漸近線的方程為
|
| [ ] |
A. |
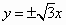
|
B. |
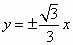
|
C. |
y=±3x
|
D. |
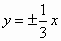
|
|
|
查看答案和解析>>
