
由世界自然基金會發(fā)起的“地球1小時”活動,已發(fā)展成為最有影響力的環(huán)保活動之一,今年的參與人數再創(chuàng)新高.然而也有部分公眾對該活動的實際效果與負面影響提出了疑問.對此,某新聞媒體進行了網上調查,所有參與調查的人中,持“支持”、“保留”和“不支持”態(tài)度的人數如下表所示:
| | 支持 | 保留 | 不支持 |
| 20歲以下 | 800 | 450 | 200 |
| 20歲以上(含20歲) | 100 | 150 | 300 |
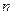 個人,已知從“支持”態(tài)度的人中抽取了45人,求
個人,已知從“支持”態(tài)度的人中抽取了45人,求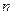 的值;
的值;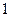 人20歲以下的概率;
人20歲以下的概率;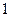 個數,求該數與總體平均數之差的絕對值超過0.6的概率.
個數,求該數與總體平均數之差的絕對值超過0.6的概率. 解:(Ⅰ)由題意得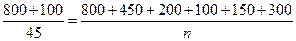 , ……………2分
, ……………2分
所以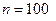 . ……………3分
. ……………3分
(Ⅱ)設所選取的人中,有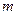 人20歲以下,則
人20歲以下,則 ,解得
,解得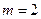 .………5分
.………5分
也就是20歲以下抽取了2人,另一部分抽取了3人,分別記作A1,A2;B1,B2,B3,
則從中任取2人的所有基本事件為 (A1,B1),(A1, B2),(A1, B3),(A2 ,B1),(A2 ,B2),(A2 ,B3),(A1, A2),(B1 ,B2),(B2 ,B3),(B1 ,B3)共10個. ………7分
其中至少有1人20歲以下的基本事件有7個:(A1, B1),(A1, B2),(A1, B3),(A2 ,B1),(A2 ,B2),(A2 ,B3),(A1, A2), …………8分
所以從中任意抽取2人,至少有1人20歲以下的概率為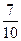 . ……………9分
. ……………9分
(Ⅲ)總體的平均數為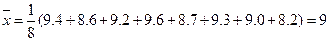 ,………10分
,………10分
那么與總體平均數之差的絕對值超過0.6的數只有8.2, ……………12分
所以該數與總體平均數之差的絕對值超過0.6的概率為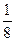 . ……………13分
. ……………13分
解析


 寒假學與練系列答案
寒假學與練系列答案科目:高中數學 來源: 題型:解答題
(本小題滿分12分)
某班50位學生期中考試數學成績的頻率分布直方圖如圖所示,成績分組區(qū)間是:[40,50)、[50,60)、[60,70)、[70,80)、[80,90)、[90,100].
(Ⅰ)求圖中 x的值;
(Ⅱ)從成績不低于80分的學生中隨機選取2人,該2人中成績在90分以上(含90分)的人數記為ξ,求ξ的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分12分)
為了比較注射A,B兩種藥物后產生的皮膚皰疹的面積,選200只家兔做實驗,將這200只家兔隨機地分成兩組。每組100只,其中一組注射藥物A,另一組注射藥物B。下表1和表2分別是注射藥物A和藥物B后的實驗結果。(皰疹面積單位: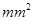 )
)
完成下面頻率分布直方圖,并比較注射兩種藥物后皰疹面積的中位數大小;
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某網站欲調查網民對當前網頁的滿意程度,在登錄的所有網民中,收回有效帖子
50000份,其中持各種態(tài)度的份數如下表所示.
很滿 意 意 | 滿意 | 一般 | 不滿意 |
| 10800 | 12400 | 15600 | 11200 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
一個總體中的1000個個體編號為0,1,2,…,999,并依次將其分為10個小組,組號為0,1,2,…,9,要用系統(tǒng)抽樣方法抽取一個容量為10的樣本,規(guī)定如果在第0組隨機抽取的號碼為x,那么依次錯位地得到后面各組的號碼,即第k組中抽取的號碼的后兩位數為x+33k的后兩位數.
(1)當x=24時,寫出所抽取樣本的10個號碼;
(2)若所抽取樣本的10個號碼中有一個的后兩位數是87,求x的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
為了調查甲、乙兩個網站受歡迎的程度,隨機選取了14天,統(tǒng)計上午8:00—10:00間各自的點 擊量,得如右所示的統(tǒng)計圖,根據統(tǒng)計圖:
擊量,得如右所示的統(tǒng)計圖,根據統(tǒng)計圖: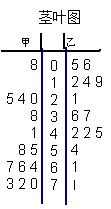
(1)甲、乙兩個網站點擊量的極差分別是多少?
(2)甲網站點擊量在[10,40]間的頻率是多少?
(3)甲、乙兩個網站哪個更受歡迎?并說明理由。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
下表是關于某設備的使用年限(年)和所需要的維修費用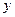 (萬元)的幾組統(tǒng)計數據:
(萬元)的幾組統(tǒng)計數據:
 | 2 | 3 | 4 | 5 | 6 |
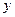 | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
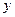 關于
關于 的線性回歸方程
的線性回歸方程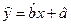 ;
;


查看答案和解析>>
科目:高中數學 來源: 題型:解答題
甲,乙兩機床同時加工直徑為100cm的零件,為檢驗質量,各從中抽取6件測量的數據為:甲:99,100,98,100,100,103 乙:99,100, 102, 99,100 ,100
(1)分別計算兩組數據的平均數及方差
(2)根據計算結果判斷哪臺機床加工零件的質量更穩(wěn)定.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分為12分)
某中學研究性學習小組,為了考察高中學生的作文水平與愛看課外書的關系,在本校高三年級隨機調查了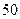 名學生。調査結果表明:在愛看課外書的
名學生。調査結果表明:在愛看課外書的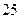 人中有
人中有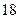 人作文水平好,另
人作文水平好,另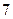 人作文水平一般;在不愛看課外書的
人作文水平一般;在不愛看課外書的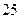 人中有
人中有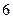 人作文水平好,另
人作文水平好,另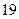 人作文水平一般.
人作文水平一般.
(Ⅰ)試根據以上數據建立一個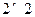 列聯(lián)表,并運用獨立性檢驗思想,指出有多大把握認為中學生的作文
列聯(lián)表,并運用獨立性檢驗思想,指出有多大把握認為中學生的作文 水平與愛看課外書有關系?
水平與愛看課外書有關系?
(Ⅱ)將其中某5名愛看課外書且作文水平好的學生分別編號為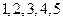 ,某
,某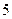 名愛看
名愛看 課外書且作文水平一般的學生也分別編號為
課外書且作文水平一般的學生也分別編號為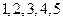 ,從這兩組學生中各任選
,從這兩組學生中各任選 人進行學習交流,求被選取的兩名學生的編號之和為
人進行學習交流,求被選取的兩名學生的編號之和為 的倍數或
的倍數或 的倍數的概率.
的倍數的概率.
附: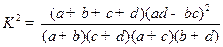
臨界值表:
 | 0. 10 | 0. 05 | 0. 025 | 0.010 | 0. 005 | 0. 001 |
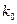 | 2. 706 | 3. 841 | 5. 024 | 6. 635 | 7. 879 | 10. 828 |
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com