
(Ⅰ)求動點Q的軌跡方程;
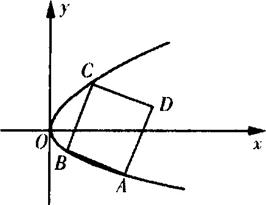
(Ⅱ)若正方體ABCD的三個頂點A、B、C在點Q的軌跡上,求正方形ABCD面積的最小值.
解:(Ⅰ)設Q(x,y),因為![]() =
=![]()
![]() ,所以N(0,
,所以N(0,![]() ),
),
又M(-3m,0),所以![]() =(3m,
=(3m,![]() ),
),![]() =(x,
=(x,![]() ),
),
由已知![]() ·
·![]() =0,則3mx-
=0,則3mx-![]() y2=0,y2=4mx.
y2=0,y2=4mx.
即Q點軌跡方程為y2=4mx.
(Ⅱ)如圖,不妨設正方形在拋物線上的三個頂點中A、B在x軸的下方(包括x軸),記A、B、C的坐標分別為(x1,y1),(x2,y2),(x3,y3),其中y3>0≥y2>y1

并設直線AB的斜率為k(k<0)
則有 ①
①
又因為A、B、C在拋物線y2=4mx上,故有
x1=![]() ,x2=
,x2=![]() ,x3=
,x3=![]() 代入①式得
代入①式得
y1=![]() -y2,y3=-4mk-y2②
-y2,y3=-4mk-y2②
∵|AB|=|BC|
即![]()
∴![]() (y2- y1)=
(y2- y1)=![]() (y3-y2)
(y3-y2)
∴(y2-y1)=-k(y3-y2)將②代入可得:
y2-![]() +y2=-k(-4mk-2y2)
+y2=-k(-4mk-2y2)
即-4mk2-![]() =-2(-k+1)y2,得y2=
=-2(-k+1)y2,得y2=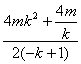
正方形的邊長為
|AB|=![]() (y3-y2)=
(y3-y2)=![]() (-4mk-2y2)
(-4mk-2y2)
=![]() (-4mk-
(-4mk-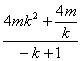 )
)
=4m![]() [-k-
[-k-![]() ]
]
=4m![]()
易知![]() ≥2,
≥2,![]() ≥
≥![]()
所以4m![]() ≥4
≥4![]() m
m
所以正方形ABCD面積的最小值為32m2.


科目:高中數學 來源:天利38套《2008全國各省市高考模擬試題匯編 精華大字版》、數學理 題型:044
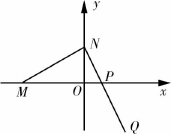
如圖,已知M(-3m,0)(m>0),N、P兩點分別在y軸和x軸上運動,并且滿足![]() ·
·![]() =0,
=0,![]() =
=![]()
![]() .
.
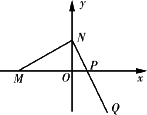
(Ⅰ)求動點Q的軌跡方程;
(Ⅱ)若正方形ABCD的三個頂點A、B、C在點Q的軌跡上,求正方形ABCD面積的最小值.
查看答案和解析>>
科目:高中數學 來源:天利38套《2008全國各省市高考模擬試題匯編 精華大字版》、數學文 精華大字版 題型:044
如圖,已知M(-3m,0)(m>0),N、P兩點分別在y軸和x軸上運動,并且滿足![]()
(Ⅰ)求動點Q的軌跡方程;
(Ⅱ)若正方體ABCD的三個頂點A、B、C在點Q的軌跡上,求正方形ABCD面積的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:

(1)畫出這個空間直角坐標系,并指出![]() 與Ox的軸的正方向的夾角;
與Ox的軸的正方向的夾角;
(2)求證:![]() ⊥
⊥![]() ;
;
(3)若M為BC的中點,n=![]() m,求直線AM與平面PBC所成角的大小.
m,求直線AM與平面PBC所成角的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
(Ⅰ)求動點Q的軌跡方程;
(Ⅱ)若正方形ABCD的三個頂點A、B、C在點Q的軌跡上,求正方形ABCD面積的最小值.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com