
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源:不詳 題型:解答題
| 學歷 | 35歲以下 | 35至50歲 | 50歲以上 |
| 本科 | 80 | 30 | 20 |
| 研究生 | x | 20 | y |
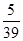 ,求x、y的值.
,求x、y的值.查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
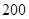 個樣品,并對其壽命進行追蹤調查,將結果列成頻率分布表如下.根據壽命將燈泡分成優等品、正品和次品三個等級,其中壽命大于或等于
個樣品,并對其壽命進行追蹤調查,將結果列成頻率分布表如下.根據壽命將燈泡分成優等品、正品和次品三個等級,其中壽命大于或等于 天的燈泡是優等品,壽命小于
天的燈泡是優等品,壽命小于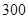 天的燈泡是次品,其余的燈泡是正品.
天的燈泡是次品,其余的燈泡是正品.| 壽命(天) | 頻數 | 頻率 |
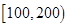 | 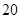 | 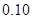 |
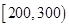 | 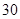 | 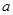 |
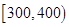 | 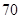 | 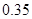 |
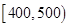 | 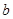 | 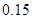 |
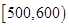 | 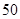 | 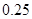 |
| 合計 | 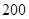 | 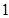 |
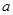 、
、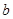 的值;
的值;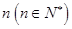 個,如果這
個,如果這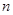 個燈泡的等級情況恰好與按三個等級分層抽樣所得的結果相同,求
個燈泡的等級情況恰好與按三個等級分層抽樣所得的結果相同,求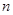 的最小值;
的最小值;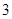 個進行使用,若以上述頻率作為概率,用
個進行使用,若以上述頻率作為概率,用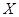 表示此人所購買的燈泡中次品的個數,求
表示此人所購買的燈泡中次品的個數,求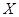 的分布列和數學期望.
的分布列和數學期望.查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
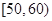 ,
,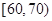 ,
,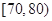 ,
,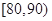 ,
,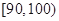 分別加以統計,得到如圖所示的頻率分布直方圖.
分別加以統計,得到如圖所示的頻率分布直方圖.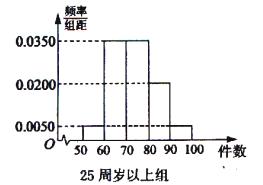
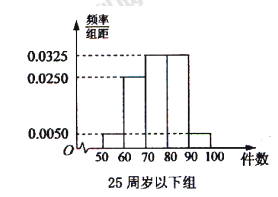

 的列聯表,并判斷是否有
的列聯表,并判斷是否有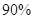 的把握認為“生產能手與工人所在的年齡組有關”?
的把握認為“生產能手與工人所在的年齡組有關”?
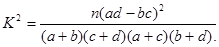
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
 名男生和
名男生和 名女生進行了不記名的問卷調查,得到了如下的統計結果:
名女生進行了不記名的問卷調查,得到了如下的統計結果:| 上網時間(分鐘) |  |  |  |  |  |
| 人數 | 5 | 25 | 30 | 25 | 15 |
| 上網時間(分鐘) |  |  |  |  |  |
| 人數 | 10 | 20 | 40 | 20 | 10 |
 列聯表,并回答能否有90%的把握認為“學生周日上網時間與性別有關”?
列聯表,并回答能否有90%的把握認為“學生周日上網時間與性別有關”?| | 上網時間少于60分鐘 | 上網時間不少于60分鐘 | 合計 |
| 男生 | | | |
| 女生 | | | |
| 合計 | | | |
 ,其中
,其中
 | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
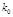 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |
查看答案和解析>>
科目:高中數學 來源:不詳 題型:單選題
| 7816 6572 0802 6314 0702 4369 9728 0198 |
| 3204 9234 4934 8200 3623 4869 6938 7481 |
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
| 年份 | 1985 | 1986 | 1987 | 1988 | 1989 | 1990 | 1991 | 1992 |
| x(kg) | 70 | 74 | 80 | 78 | 85 | 92 | 90 | 95 |
| y(t) | 5.1 | 6.0 | 6.8 | 7.8 | 9.0 | 10.2 | 10.0 | 12.0 |
| | ||||||||
| 年份 | 1993 | 1994 | 1995 | 1996 | 1997 | 1998 | 1999 | |
| x(kg) | 92 | 108 | 115 | 123 | 130 | 138 | 145 | |
| y(t) | 11.5 | 11.0 | 11.8 | 12.2 | 12.5 | 12.8 | 13.0 | |
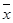 =101,
=101,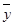 ≈10.113 3,
≈10.113 3,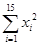 =161 125,
=161 125,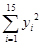 =1 628.55,
=1 628.55,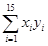 =16 076.8)
=16 076.8)查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
| | 又發作過心臟病 | 未發作過心臟病 | 合計 |
| 心臟搭橋手術 | 39 | 157 | 196 |
| 血管清障手術 | 29 | 167 | 196 |
| 合計 | 68 | 324 | 392 |
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com