已知△ABC的三個頂點為A(4,1)、B(7,5)、C(3,7)
(1)求BC邊上的垂直平分線所在直線的方程.
(2)求△ABC的面積.
解:(1)由題意可得BC的中點為(5,6),
而且BC的斜率為
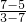
=

,
故垂直平分線的斜率為2
故直線的方程為:y-6=2(x-5),
化為一般式可得2x-y-4=0,
故BC邊上的垂直平分線所在直線的方程為2x-y-4=0;
(2)由(1)可知BC的斜率為

,故BC的方程為y-5=

(x-7)
化為一般式可得x+2y-17=0,故點A(4,1)到直線BC的距離為
d=
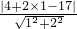
=
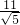
,
由距離公式可得BC=
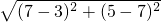
=

,
故△ABC的面積為

=11
分析:(1)由題意可得BC的中點和BC的斜率,由垂直關系可得垂直平分線的斜率,由點斜式可得方程,化為一般式即可;
(2)由(1)可得BC的方程,可得A到BC的距離,再求得BC的長度,代入三角形的面積公式可得答案.
點評:本題考查直線的一般式方程和垂直關系,涉及點到直線的距離,屬基礎題.

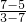 =
= ,
, ,故BC的方程為y-5=
,故BC的方程為y-5= (x-7)
(x-7)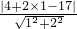 =
=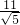 ,
,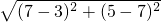 =
= ,
, =11
=11
