
某農科所對冬季晝夜溫差大小與某反季節大豆新品種發芽多少之間的關系進行分析研究,他們分別記錄了12月1日至12月5日的每天晝夜溫差與實驗室每天每100顆種子中的發芽數,得到如下資料:
| 日期 | 12月1日 | 12月2日 | 12月3日 | 12月4日 | 12月5日 |
| 溫差x/℃ | 10 | 11 | 13 | 12 | 8 |
| 發芽數y /顆 | 23 | 25 | 30 | 26 | 16 |
 =bx+a;
=bx+a; 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:解答題
下表是某市從3月份中隨機抽取的 天空氣質量指數(
天空氣質量指數( )和“
)和“ ”(直徑小于等于
”(直徑小于等于 微米的顆粒物)
微米的顆粒物) 小時平均濃度的數據,空氣質量指數(
小時平均濃度的數據,空氣質量指數( )小于
)小于 表示空氣質量優良.
表示空氣質量優良.
| 日期編號 |  |  |  |  |  |  |  |  |  |  |
空氣質量指數( ) ) |  |  |  |  |  |  |  |  |  |  |
“ ” ” 小時平均濃度( 小時平均濃度( ) ) |  |  |  |  |  |  |  |  |  |  |
 為“抽取的兩個日期中,當天‘
為“抽取的兩個日期中,當天‘ ’的
’的 小時平均濃度不超過
小時平均濃度不超過 ”,求事件
”,求事件 發生的概率;
發生的概率; 天,記
天,記 為“
為“ ”
” 小時平均濃度不超過
小時平均濃度不超過 的天數,求
的天數,求 的分布列和數學期望.
的分布列和數學期望.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某市規定,高中學生三年在校期間參加不少于 小時的社區服務才合格.教育部門在全市隨機抽取200位學生參加社區服務的數據,按時間段
小時的社區服務才合格.教育部門在全市隨機抽取200位學生參加社區服務的數據,按時間段 ,
, ,
, ,
, ,
, (單位:小時)進行統計,其頻率分布直方圖如圖所示.
(單位:小時)進行統計,其頻率分布直方圖如圖所示.
(Ⅰ)求抽取的200位學生中,參加社區服務時間不少于90小時的學生人數,并估計
從全市高中學生中任意選取一人,其參加社區服務時間不少于90小時的概率;
(Ⅱ)從全市高中學生(人數很多)中任意選取3位學生,記 為3位學生中參加社區服務時間不少于90小時的人數.試求隨機變量
為3位學生中參加社區服務時間不少于90小時的人數.試求隨機變量 的分布列和數學期望
的分布列和數學期望 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
一個盒子中裝有大量形狀大小一樣但重量不盡相同的小球,從中隨機抽取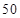 個作為樣本,稱出它們的重量(單位:克),重量分組區間為
個作為樣本,稱出它們的重量(單位:克),重量分組區間為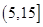 ,
,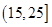 ,
,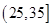 ,
, ,由此得到樣本的重量頻率分布直方圖,如圖
,由此得到樣本的重量頻率分布直方圖,如圖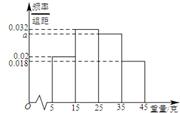
(1)求 的值;
的值;
(2)根據樣本數據,試估計盒子中小球重量的平均值;
(注:設樣本數據第 組的頻率為
組的頻率為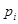 ,第
,第 組區間的中點值為
組區間的中點值為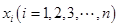 ,則樣本數據的平均值為
,則樣本數據的平均值為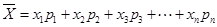 .)
.)
(3)從盒子中隨機抽取 個小球,其中重量在
個小球,其中重量在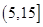 內的小球個數為
內的小球個數為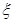 ,求
,求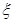 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
通過隨機詢問110名不同的大學生是否愛好某項運動,得到如下的列聯表:
| | 男 | 女 | 總計 |
| 愛好 | 40 | 20 | 60 |
| 不愛好 | 20 | 30 | 50 |
| 總計 | 60 | 50 | 110 |
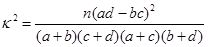
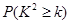 | 0.050 | 0.010 | 0.001 |
 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某商場經營一批進價是30元/臺的小商品,在市場試驗中發現,此商品的銷售單價x(x取整數)元與日銷售量y臺之間有如下關系:
| x | 35 | 40 | 45 | 50 |
| y | 56 | 41 | 28 | 11 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某產品的三個質量指標分別為x,y,z,用綜合指標S=x+y+z評價該產品的等級.若S≤4,則該產品為一等品.先從一批該產品中,隨機抽取10件產品作為樣本,其質量指標列表如下:
| 產品編號 | A1 | A2 | A3 | A4 | A5 |
| 質量指標(x,y,z) | (1,1,2) | (2,1,1) | (2,2,2) | (1,1,1) | (1,2,1) |
| 產品編號 | A6 | A7 | A8 | A9 | A10 |
| 質量指標(x,y,z) | (1,2,2) | (2,1,1) | (2,2,1) | (1,1,1) | (2,1,2) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某化肥廠有甲、乙兩個車間包裝肥料,在自動包裝傳送帶上每隔30分鐘抽取一包產品,稱其重量(單位:kg),分別記錄抽查數據如下:
甲:102,101,99,98,103,98,99;
乙:110,115,90,85,75,115,110.
(1)這種抽樣方法是哪一種方法?
(2)試計算甲、乙車間產品重量的平均數與方差,并說明哪個車間產品較穩定?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
根據空氣質量指數API(為整數)的不同,可將空氣質量分級如下表:
| API | 0~50 | 51~ 100 | 101~ 150 | 151~ 200 | 201~ 250 | 251~ 300 | >300 |
| 級 別 | Ⅰ | Ⅱ | Ⅲ1 | Ⅲ2 | Ⅳ1 | Ⅳ2 | Ⅴ |
| 狀 況 | 優 | 良 | 輕微 污染 | 輕度 污染 | 中度 污染 | 中度 重污染 | 重度 污染 |
| |  |  |  |  |  | ||

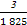 +
+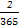 +
+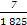 +
+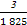 +
+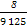 =
=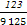 ,365=73×5).
,365=73×5).查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com