
 .再由 f′(1)=0,利用函數的周期性求出方程f′(x)=0在區間[0,6]上的實根,從而得出結論.
.再由 f′(1)=0,利用函數的周期性求出方程f′(x)=0在區間[0,6]上的實根,從而得出結論. )=f(x-
)=f(x- )=f(
)=f( -x),
-x), 對稱,且函數f′(x)是奇函數,且周期等于
對稱,且函數f′(x)是奇函數,且周期等于 .
. )=f'(3)=0.
)=f'(3)=0. 以及 f′(1)=0,求得 f′(
以及 f′(1)=0,求得 f′( )=f′(4)=f′(
)=f′(4)=f′( )=f′(
)=f′(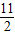 )=f′(6)=0.
)=f′(6)=0. ,1,
,1, ,3,4,
,3,4, ,
,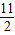 ,6,共有9個,
,6,共有9個,

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com