
某人有4種顏色的燈泡(每種顏色的燈泡足夠多),要在 如圖所示的三棱臺6個頂點 ,
, ,
, ,
, ,
, ,
, 上 各裝一個燈泡,要求同一條線段兩端的燈泡不同色,則不同的安裝方法共有
種(用數字作答).
上 各裝一個燈泡,要求同一條線段兩端的燈泡不同色,則不同的安裝方法共有
種(用數字作答).

264
【解析】解:∵至少用了三種顏色的燈泡安裝.
∴可能用了三種顏色安裝,可能用了四種顏色安裝.
由分類計數原理,可分兩類:
第一類,用了三種顏色安裝,
第一步,為A、B、C三點選三種顏色燈泡共有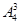 種選法;第二步,為A1點選一種顏色共有不同于A點的2種選法;第三步,為B1、C1選燈泡,共有1種選法
種選法;第二步,為A1點選一種顏色共有不同于A點的2種選法;第三步,為B1、C1選燈泡,共有1種選法
∴第一類共有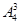 ×2×1=48種方法.
×2×1=48種方法.
第二類,用了四種顏色安裝,
第一步,為A、B、C三點選三種顏色燈泡共有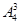 種選法;第二步,為A1點選一種顏色共有不同于A點的3種選法;第三步,為B1、C1選燈泡:若B1與A同色,則C1只能選B點顏色;若B1與C同色,則C1有A、B處兩種顏色可選.故為B1、C1選燈泡共有3種選法
種選法;第二步,為A1點選一種顏色共有不同于A點的3種選法;第三步,為B1、C1選燈泡:若B1與A同色,則C1只能選B點顏色;若B1與C同色,則C1有A、B處兩種顏色可選.故為B1、C1選燈泡共有3種選法
∴第二類共有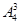 ×3×3=216種方法.
×3×3=216種方法.
綜上所述,至少用了三種顏色的燈泡的安裝方法共有48+216=264種方法
故答案為 264


 教學練新同步練習系列答案
教學練新同步練習系列答案 課前課后同步練習系列答案
課前課后同步練習系列答案科目:高中數學 來源: 題型:
 16、某人有4種顏色的燈泡(每種顏色的燈泡足夠多),要在如圖所示的6個點A、B、C、A1、B1、C1上各裝一個燈泡,要求同一條線段兩端的燈泡不同色,則每種顏色的燈泡都至少用一個的安裝方法共有
16、某人有4種顏色的燈泡(每種顏色的燈泡足夠多),要在如圖所示的6個點A、B、C、A1、B1、C1上各裝一個燈泡,要求同一條線段兩端的燈泡不同色,則每種顏色的燈泡都至少用一個的安裝方法共有查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
 某人有4種顏色的燈泡(每種顏色的燈泡足夠多),要在如圖所示的6個點A、B、C、A1、B1、C1上各裝一個燈泡,要求同一條線段兩端的燈泡不同色,則每種顏色的燈泡都至少用一個的安裝方法共有( )種.
某人有4種顏色的燈泡(每種顏色的燈泡足夠多),要在如圖所示的6個點A、B、C、A1、B1、C1上各裝一個燈泡,要求同一條線段兩端的燈泡不同色,則每種顏色的燈泡都至少用一個的安裝方法共有( )種.查看答案和解析>>
科目:高中數學 來源: 題型:
 某人有4種顏色的燈泡(每種顏色的燈泡足夠多),要在如圖三棱柱ABC-A1B1C1的六個頂點上各安裝一個燈泡,要求同一條線段的兩端的燈泡顏色不同,則每種顏色的燈泡至少用一個的安裝方法共有( )
某人有4種顏色的燈泡(每種顏色的燈泡足夠多),要在如圖三棱柱ABC-A1B1C1的六個頂點上各安裝一個燈泡,要求同一條線段的兩端的燈泡顏色不同,則每種顏色的燈泡至少用一個的安裝方法共有( )查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com