中文字幕人妻色偷偷久久-精品久久久久成人码免费动漫-久久精品国产清自在天天线-国产成人精品免高潮在线观看

選修4—1：（本小題滿分10分）幾何證明選講
如圖，在△ABC中，∠C為鈍角，點E，
H分別是邊AB上的點，點K和M分別
是邊AC和BC上的點，且AH＝AC，EB
＝BC，AE＝AK，BH＝BM．   
（Ⅰ）求證：E、H、M、K四點共圓；
（Ⅱ）若KE＝EH，CE＝3，求線段KM的  
長．
證明：⑴連接，
，
四邊形為等腰梯形，
注意到等腰梯形的對角互補，
故四點共圓，----------- 3分
同理四點共圓，
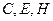
即均在點所確定的圓上，證畢．--------------- 5分
⑵連結(jié)，
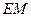
由⑴得五點共圓，----------- 7分
　為等腰梯形，，
故，
由可得，
故，
即為所求．  -------------------10分
略
練習(xí)冊系列答案
相關(guān)習(xí)題

科目：高中數(shù)學(xué) 來源：不詳 題型：填空題

如圖，在△ABC中，D是AC的中點，E是BD的中點，AE交BC于F，則             .

查看答案和解析>>

科目：高中數(shù)學(xué) 來源：不詳 題型：解答題

（本小題滿分10分）選修4-1：幾何證明選講
如圖，四邊形內(nèi)接于，，過點的切線交的延長線于點。求證：。

查看答案和解析>>

科目：高中數(shù)學(xué) 來源：不詳 題型：解答題

【選做題】本題包括A、B、C、D四小題，請選定其中兩題，并在相應(yīng)的答題區(qū)域內(nèi)作答.若多做，則按作答的前兩題評分.解答時應(yīng)寫出文字說明、證明過程或演算步驟．
A. 選修4－1：幾何證明選講
(本小題滿分10分)
如圖，與⊙相切于點，為的中點，
過點引割線交⊙于，兩點，
求證: ．

查看答案和解析>>

科目：高中數(shù)學(xué) 來源：不詳 題型：解答題

（本小題滿分12分）如圖，在等腰梯形ABCD中，AD∥BC，AB=DC，過點D作AC的平行線DE，交BA的延長線于點E。
求證：（1）≌；
（2）DEDC=AEBD。

查看答案和解析>>

科目：高中數(shù)學(xué) 來源：不詳 題型：填空題

（幾何證明選講選做題）如圖，半徑為2的⊙O中，∠AOB=90°，D為OB的中點，AD的延長線交⊙O于點E，則線段DE的長為______．

查看答案和解析>>

科目：高中數(shù)學(xué) 來源：不詳 題型：填空題

已知點是的中位線上任意一點，且，實數(shù)，
滿足．設(shè)，，，的面積分別為，，，， 記，，．則取最大值時，的值為  ▲ ．

查看答案和解析>>

科目：高中數(shù)學(xué) 來源：不詳 題型：單選題

在直角三角形中，斜邊上的高為6cm，且把斜邊分成3︰2兩段，則斜邊上的中線的長為（  ）
A．cmB．cmC．cmD．cm

查看答案和解析>>

科目：高中數(shù)學(xué) 來源：不詳 題型：單選題

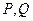
如圖,設(shè)為內(nèi)的兩點,且,＝＋,則的面積與的面積之比為(    )
A．B．C．D．

查看答案和解析>>

同步練習(xí)冊答案