
(Ⅰ)已知函數![]() .數列
.數列![]() 滿足:
滿足:![]() ,且
,且![]() ,記數列
,記數列![]() 的前
的前![]() 項和為
項和為![]() ,且
,且![]() .求數列
.求數列![]() 的通項公式;并判斷
的通項公式;并判斷![]() 是否仍為數列
是否仍為數列![]() 中的項?若是,請證明;否則,說明理由.
中的項?若是,請證明;否則,說明理由.
(Ⅱ)設![]() 為首項是
為首項是![]() ,公差
,公差![]() 的等差數列,求證:“數列
的等差數列,求證:“數列![]() 中任意不同兩項之和仍為數列
中任意不同兩項之和仍為數列![]() 中的項”的充要條件是“存在整數
中的項”的充要條件是“存在整數![]() ,使
,使![]() ”.
”.
同下
(Ⅰ)因為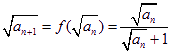 ,
,
所以![]() ,即
,即![]() ,
,
![]() ,即
,即![]() . ……………………………………(4分)
. ……………………………………(4分)
因為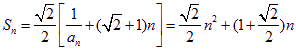 ,
,
當![]() 時,
時,![]() ,
,
當![]() 時,
時,![]() ,
,
所以![]() . …………………………(6分)
. …………………………(6分)
又因為![]() ,
,
所以令![]() ,則
,則![]()
得到![]() 與
與![]() 矛盾,所以
矛盾,所以![]() 不在數列
不在數列![]() 中. ………(8分)
中. ………(8分)
(Ⅱ)充分性:若存在整數![]() ,使
,使![]() .
.
設![]() 為數列
為數列![]() 中不同的兩項,則
中不同的兩項,則![]()
![]() .
.
又![]() 且
且![]() ,所以
,所以![]() .
.
即![]() 是數列
是數列![]() 的第
的第![]() 項. ……………………(11分)
項. ……………………(11分)
必要性:若數列![]() 中任意不同兩項之和仍為數列
中任意不同兩項之和仍為數列![]() 中的項,
中的項,
則![]() ,
,![]() ,(
,(![]() ,
,![]() 為互不相同的正整數)
為互不相同的正整數)
則![]() ,令
,令![]() ,
,
得到![]()
![]() ,
,
所以![]() ,令整數
,令整數![]() ,所以
,所以![]() . ……(14 分)
. ……(14 分)
下證整數![]()
若設整數![]() 則
則![]() .令
.令![]() ,
,
由題設取![]() 使
使![]()
即![]() ,所以
,所以![]()
即![]() 與
與![]() 相矛盾,所以
相矛盾,所以![]() .
.
綜上, 數列![]() 中任意不同兩項之和仍為數列
中任意不同兩項之和仍為數列![]() 中的項的充要條件是存在整數
中的項的充要條件是存在整數![]() ,使
,使![]() . ……………………(16分)
. ……………………(16分)


 鴻圖圖書寒假作業假期作業吉林大學出版社系列答案
鴻圖圖書寒假作業假期作業吉林大學出版社系列答案科目:高中數學 來源: 題型:
(08年聊城市四模文)(14分)已知函數![]() +
+![]() 數列{an}的首項為1,前n項和為Sn,且
數列{an}的首項為1,前n項和為Sn,且![]() ,在函數f(x)的圖像上.
,在函數f(x)的圖像上.
(1)證明:數列{an}是等差數列;
(2)若b=4,向量![]() 、
、![]() ,動點M滿足
,動點M滿足![]() ,點N是曲線
,點N是曲線![]() 上的動點,求|MN|的最小值.
上的動點,求|MN|的最小值.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年山西省高三上學期期中考試理科數學試卷(解析版) 題型:選擇題
已知函數
 數列
數列 滿足
滿足 ,且
,且 是單調遞增數列,則實數
是單調遞增數列,則實數 的取值范圍(
)
的取值范圍(
)
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中數學 來源:2014屆遼寧瓦房店高級中學高二上期中考試理科數學試卷(解析版) 題型:解答題
(本題滿分12分)已知函數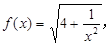 數列
數列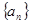 的前n項和為
的前n項和為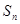 ,
,
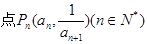 ,在曲線
,在曲線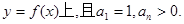
(1)求數列{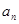 }的通項公式
}的通項公式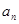 ;(II)數列{
;(II)數列{ }首項b1=1,前n項和Tn,且
}首項b1=1,前n項和Tn,且
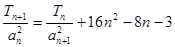 ,求數列{
,求數列{ }通項公式bn.
}通項公式bn.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com