Question

已知二面角α－l－β的大小為50°，P為空間中任意一點，則過點P且與平面α和平面β所成的角都是25°的直線的條數為(　　)

A．2

B．3

C． 4

D．5

Answer 1

B

分析：利用線面角的概念及角平分線的性質，分析出所求直線二面角的平分面上，再根據線面角的大小變化確定出直線條數．
解：首先給出下面兩個結論
①兩條平行線與同一個平面所成的角相等．
②與二面角的兩個面成等角的直線在二面角的平分面上．
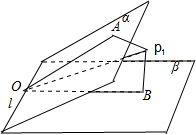
圖1．
（1）如圖1，過二面角α-l-β內任一點作棱l的垂面AOB，交棱于點O，與兩半平面于OA，OB，則∠AOB為二面角α-l-β的平面角，∠AOB=50°
設OP₁為∠AOB的平分線，則∠P₁OA=∠P₁OB=25°，與平面α，β所成的角都是25°，此時過P且與OP₁平行的直線符合要求，有一條．當OP₁以O為軸心，在二面角α-l-β的平分面上轉動時，OP₁與兩平面夾角變小，不再會出現25°情形．
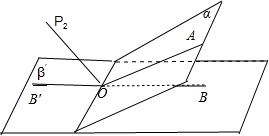
圖2．
（2）如圖2，設OP₂為∠AOB的補角∠AOB′，則∠P₂OA=∠P₂OB=65°，與平面α，β所成的角都是65°．當OP₂以O為軸心，在二面角α-l-β′的平分面上轉動時，OP₂與兩平面夾角變小，對稱地在圖中OP₂兩側會出現25°情形，有兩條．此時過P且與OP₂平行的直線符合要求，有兩條．
綜上所述，直線的條數共有三條．
故選B．