
(08年福建卷理)(本小題滿(mǎn)分12分)
如圖,在四棱錐![]() 中,則面PAD⊥底面
中,則面PAD⊥底面![]() ,側(cè)棱
,側(cè)棱![]() ,底面
,底面![]() 為直角梯形,其中
為直角梯形,其中![]()
![]() ,
,![]() ,O為
,O為![]() 中點(diǎn)。
中點(diǎn)。
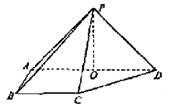
(Ⅰ)求證:PO⊥平面![]() ;
;
(Ⅱ)求異面直線(xiàn)PB與CD所成角的大小;
(Ⅲ)線(xiàn)段AD上是否存在點(diǎn)Q,使得它到平面PCD的距離為![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,請(qǐng)說(shuō)明理由.
的值;若不存在,請(qǐng)說(shuō)明理由.
解析:
解法一:
(Ⅰ)證明:在△PAD中PA=PD,O為AD中點(diǎn),所以PO⊥AD,
又側(cè)面PAD⊥底面ABCD,平面![]() 平面ABCD=AD,
平面ABCD=AD,![]() 平面PAD,
平面PAD,
所以PO⊥平面ABCD.
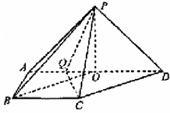
(Ⅱ)連結(jié)BO,在直角梯形ABCD中,BC∥AD,![]() ,
,
有OD∥BC且OD=BC,所以四邊形OBCD是平行四邊形,所以OB∥DC.
由(Ⅰ)知,PO⊥OB,∠PBO為銳角,
所以∠PBO是異面直線(xiàn)PB與CD所成的角.
因?yàn)?IMG src='http://thumb.zyjl.cn/pic1/img/20090323/20090323142608005.gif' width=144 height=19>,
在Rt△AOB中,AB=1,AO=1,
所以OB=![]() ,
,
在Rt△POA中,因?yàn)?I>AP=![]() ,AO=1,所以OP=1,
,AO=1,所以OP=1,
在Rt△PBO中,tan∠PBO=![]()
所以異面直線(xiàn)PB與CD所成的角是![]() .
.
(Ⅲ)假設(shè)存在點(diǎn)Q,使得它到平面PCD的距離為![]() .
.
設(shè)![]() ,則
,則![]() ,由(Ⅱ)得CD=OB=
,由(Ⅱ)得CD=OB=![]() ,
,
在Rt△POC中, ![]()
所以PC=CD=DP, ![]()
由![]() 得
得![]() ,解得
,解得![]() ,
,
所以存在點(diǎn)Q滿(mǎn)足題意,此時(shí)![]() .
.
解法二:
(Ⅰ)同解法一.
(Ⅱ)以![]() 為坐標(biāo)原點(diǎn),
為坐標(biāo)原點(diǎn),![]() 的方向分別為x軸、y軸、z軸的正方向,建立空間直角坐標(biāo)系
的方向分別為x軸、y軸、z軸的正方向,建立空間直角坐標(biāo)系![]() ,依題意,易得
,依題意,易得![]() ,
,
所以![]()
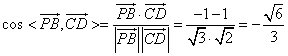 .
.
所以異面直線(xiàn)![]() 與
與![]() 所成的角是
所成的角是![]() .
.
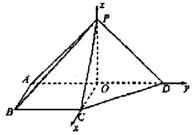
(Ⅲ)假設(shè)存在點(diǎn)![]() ,使得它到平面PCD的距離為
,使得它到平面PCD的距離為![]() ,
,
由(Ⅱ)知![]()
設(shè)平面![]() 的法向量為
的法向量為![]() .
.
則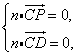 所以
所以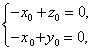 即
即![]() ,
,
取![]() ,得平面PCD的一個(gè)法向量為
,得平面PCD的一個(gè)法向量為![]() .
.
設(shè)![]() 由
由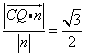 ,得
,得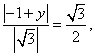
解![]() 或
或![]() (舍去),此時(shí)
(舍去),此時(shí)![]() ,
,
所以存在點(diǎn)Q滿(mǎn)足題意,此時(shí)![]() .
.
【高考考點(diǎn)】本小題主要考查直線(xiàn)與平面位置關(guān)系、異面直線(xiàn)所成角、點(diǎn)到平面的距離等基本知識(shí),考查空間想象能力、邏輯思維能力和運(yùn)算能力。
【易錯(cuò)提醒】第一問(wèn)就建立坐標(biāo)系的就會(huì)導(dǎo)致錯(cuò)誤.再者就是線(xiàn)與線(xiàn)所成角應(yīng)該在![]() 才可
才可
【備考提示】因?yàn)榱椎碾y度一再降低,所以一定要求學(xué)生掌握坐標(biāo)法,勞記公式.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
(08年福建卷理)(本小題滿(mǎn)分12分)
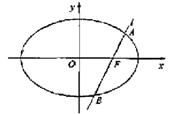
如圖,橢圓![]() 的一個(gè)焦點(diǎn)是
的一個(gè)焦點(diǎn)是![]() ,O為坐標(biāo)原點(diǎn).
,O為坐標(biāo)原點(diǎn).
(Ⅰ)已知橢圓短軸的兩個(gè)三等分點(diǎn)與一個(gè)焦點(diǎn)構(gòu)成正三角
形,求橢圓的方程;
(Ⅱ)設(shè)過(guò)點(diǎn)F的直線(xiàn)l交橢圓于A、B兩點(diǎn).若直線(xiàn)l繞點(diǎn)F
任意轉(zhuǎn)動(dòng),恒有![]() ,求a的取值范圍.
,求a的取值范圍.

查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
(08年福建卷理)(本小題滿(mǎn)分12分)
如圖,橢圓![]() 的一個(gè)焦點(diǎn)是
的一個(gè)焦點(diǎn)是![]() ,O為坐標(biāo)原點(diǎn).
,O為坐標(biāo)原點(diǎn).
(Ⅰ)已知橢圓短軸的兩個(gè)三等分點(diǎn)與一個(gè)焦點(diǎn)構(gòu)成正三角
形,求橢圓的方程;
(Ⅱ)設(shè)過(guò)點(diǎn)F的直線(xiàn)l交橢圓于A、B兩點(diǎn).若直線(xiàn)l繞點(diǎn)F
任意轉(zhuǎn)動(dòng),恒有![]() ,求a的取值范圍.
,求a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
(08年福建卷理)(本小題滿(mǎn)分12分)
某項(xiàng)考試按科目A、科目B依次進(jìn)行,只有當(dāng)科目A成績(jī)合格時(shí),才可繼續(xù)參加科
目B的考試。已知每個(gè)科目只允許有一次補(bǔ)考機(jī)會(huì),兩個(gè)科目成績(jī)均合格方可獲得證書(shū)。現(xiàn)某人參加這項(xiàng)考試,科目A每次考試成績(jī)合格的概率均為![]() ,科目B每次考試成績(jī)合格的概率均為
,科目B每次考試成績(jī)合格的概率均為![]() .假設(shè)各次考試成績(jī)合格與否均互不影響.
.假設(shè)各次考試成績(jī)合格與否均互不影響.
(Ⅰ)求他不需要補(bǔ)考就可獲得證書(shū)的概率;
(Ⅱ)在這項(xiàng)考試過(guò)程中,假設(shè)他不放棄所有的考試機(jī)會(huì),記他參加考試的次數(shù)為![]() ,求
,求![]() 的數(shù)學(xué)期望E
的數(shù)學(xué)期望E![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
(08年福建卷理)(本小題滿(mǎn)分12分)
已知函數(shù)![]() .
.
(Ⅰ)設(shè)![]() 是正數(shù)組成的數(shù)列,前n項(xiàng)和為
是正數(shù)組成的數(shù)列,前n項(xiàng)和為![]() ,其中
,其中![]() .若點(diǎn)
.若點(diǎn)![]() (n∈N*)在函數(shù)
(n∈N*)在函數(shù)![]() 的圖象上,求證:點(diǎn)
的圖象上,求證:點(diǎn)![]() 也在
也在![]() 的圖象上;
的圖象上;
(Ⅱ)求函數(shù)![]() 在區(qū)間
在區(qū)間![]() 內(nèi)的極值.
內(nèi)的極值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
(08年福建卷理)(本小題滿(mǎn)分12分)
如圖,在四棱錐![]() 中,則面PAD⊥底面
中,則面PAD⊥底面![]() ,側(cè)棱
,側(cè)棱![]() ,底面
,底面![]() 為直角梯形,其中
為直角梯形,其中![]()
![]() ,
,![]() ,O為
,O為![]() 中點(diǎn)。
中點(diǎn)。
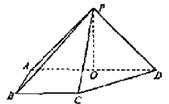
(Ⅰ)求證:PO⊥平面![]() ;
;
(Ⅱ)求異面直線(xiàn)PD與CD所成角的大小;
(Ⅲ)線(xiàn)段AD上是否存在點(diǎn)Q,使得它到平面PCD的距離為![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,請(qǐng)說(shuō)明理由.
的值;若不存在,請(qǐng)說(shuō)明理由.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com