Question

已知f(x)=(x-1)²,g(x)=10(x-1),數列{a_N}滿足a₁=2,(a_n+1-a_n)

g(a_n)+f(a_n)=0,b_n=(N+2)(a_n-1).

(1)求證：數列{a_n-1}是等比數列.

(2)當N取何值時b_n取最大值?請求出最大值.

(3)若＜對任意M∈N^*恒成立，求實數t的取值范圍.?

Answer 1

(1)證明：∵(a_n+1-a_n)g(a_n)+f(a_n)=0,f(a_n)=(a_n-1)²,g(a_n)=10(a_n-1),?

∴(a_n+1-a_n)×10(a_n-1)+(a_n-1)²=0,即(a_n-1)(10a_n+1-9a_n-1)=0.?

又a₁=2，可知對任何n∈N^*,a_n-1≠0,?

∴a_n+1=a_n+.                                                                                                   ?

∵,?

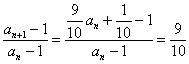∴{a_n-1}是以a₁-1=1為首項，公比為的等比數列.                                               ?

(2)解：由(1)可知a_n-1=()^n-1(n∈N^*),?

∴b_n= (n+2)(a_n-1)=(n+2)()ⁿ,?

 .                                                               ?

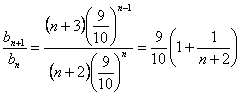當n=7時，=1,b₈=b₇;當n＜7時，＞1,b_n+1＞b_n;當n＞7時，＜1,b_n+1＜b_n.

∴當n=7或n=8時，b_n取最大值，最大值為b₇=b₈=.                                         ?

(3)解：由,得T^m［］＜0.                                               (*)?

依題意,(*)式對任意m∈N^*恒成立，?

①當T=0時，(*)式顯然不成立，因此T=0不合題意.?                                    ?

②當T＜0時，由＞0,可知T^m＜0(m∈N^*),??

而當m是偶數時T^m＞0，因此T＜0不合題意.                                                         ?

③當T＞0時，由T^m＞0(m∈N^*),?

∴＜0.?

∴T＞(m∈N^*).                                                                                       ?

設h(m)= (m∈N^*),?

∵(m+1)-h(m)= -=-·＜0,?

∴h(1)＞h(2)＞…＞h(m-1)＞h(m)＞….?

∴h(m)的最大值為h(1)=.∴實數T的取值范圍是T＞.