
選做題:請考生在第22,23,24題中任選一題做答,如果多做,則按所做的第一題記分
22.(本小題滿分10分)選修4—1幾何證明選講
如圖,AB是⊙O的直徑,AC是弦,∠BAC的平分線AD交⊙O于點D,DE⊥AC,交AC的延長線于點E,OE交AD于點F。
(I)求證:DE是⊙O的切線;
(II)若 的值.
的值.

23.(本小題滿分10分)選修4—2坐標系與參數方程
設直角坐標系原點與極坐標極點重合, x軸正半軸與極軸重合,若已知曲線C的極坐標方程為 ,點F1、F2為其左、右焦點,直線l的參數方程為
,點F1、F2為其左、右焦點,直線l的參數方程為
(I)求直線l的普通方程和曲線C的直角坐標方程;
(II)求曲線C上的動點P到直線l的最大距離。
24.(本小題滿分10分)選修4—5不等式選講
對于任意的實數 恒成立,記實數M的最大值是m。
恒成立,記實數M的最大值是m。
(1)求m的值;
(2)解不等式
略
【解析】22.(I)證明:連結OD,可得∠ODA=∠OAD=∠DAC …………2分
|
∴OE⊥OD,又OD為半徑
∴DE是的⊙O切線 …………5分
(II)解:過D作DH⊥AB于H,
則有∠DOH=∠CAB
 …………6分
…………6分
設OD=5x,則AB=10x,OH=2x,
 ………………7分
………………7分
由△AED≌△AHD可得AE=AH=7x …………8分
又由△AEF∽△DOF
可得
 …………10分
…………10分
23.解:(I)直線l普通方程為 …………3分
…………3分
橢圓C的普通方程為 …………6分
…………6分
(II)由橢圓的普通方程可以得到其參數方程為
則動點 的距離為
的距離為
 ………8分
………8分
由于 …………10分
…………10分
24.解:(I)不等式 恒成立,
恒成立,
即 對于任意的實數
對于任意的實數 恒成立,
恒成立,
只要左邊恒小于或等于右邊的最小值。 …………2分
因為 ,
,
當且僅當 時等號成立,
時等號成立,
即 成立,
成立,
也就是 的最小值是2。 …………5分
的最小值是2。 …………5分
(2) 解法1:利用絕對值的意義得:
解法1:利用絕對值的意義得:
解法2:當 ,
,
所以x的取值范圍是

解法3:構造函數
|
 的圖象,利用圖象有
的圖象,利用圖象有 得:
得:
 ………………10分
………………10分


科目:高中數學 來源: 題型:
 (2012•湖南模擬)選做題(請考生在第16題的三個小題中任選兩題作答,如果全做,則按前兩題記分,要寫出必要的推理與演算過程)
(2012•湖南模擬)選做題(請考生在第16題的三個小題中任選兩題作答,如果全做,則按前兩題記分,要寫出必要的推理與演算過程)
|
| a2 |
| x |
| b2 |
| y |
| (a+b)2 |
| x+y |
| a |
| x |
| b |
| y |
| 2 |
| x |
| 9 |
| 1-2x |
| 1 |
| 2 |
查看答案和解析>>
科目:高中數學 來源:2010年海南省高三五校聯考數學(理) 題型:解答題
選做題:請考生在第22,23,24題中任選一題做答,如果多做,則按所做的第一題記分
22.(本小題滿分10分)選修4—1幾何證明選講
如圖,AB是⊙O的直徑,AC是弦,∠BAC的平分線AD交⊙O于點D,DE⊥AC,交AC的延長線于點E,OE交AD于點F。
(I)求證:DE是⊙O的切線;
(II)若 的值.
的值.

23.(本小題滿分10分)選修4—2坐標系與參數方程
設直角坐標系原點與極坐標極點重合, x軸正半軸與極軸重合,若已知曲線C的極坐標方程為 ,點F1、F2為其左、右焦點,直線l的參數方程為
,點F1、F2為其左、右焦點,直線l的參數方程為
(I)求直線l的普通方程和曲線C的直角坐標方程;
(II)求曲線C上的動點P到直線l的最大距離。
24.(本小題滿分10分)選修4—5不等式選講
對于任意的實數 恒成立,記實數M的最大值是m。
恒成立,記實數M的最大值是m。
(1)求m的值;
(2)解不等式
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 選做題(請考生在第16題的三個小題中任選兩題作答,如果全做,則按前兩題記分,要寫出必要的推理與演算過程)
選做題(請考生在第16題的三個小題中任選兩題作答,如果全做,則按前兩題記分,要寫出必要的推理與演算過程)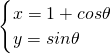 (θ為參數),求曲線C上的點到直線x-y+1=0的距離的最大值.
(θ為參數),求曲線C上的點到直線x-y+1=0的距離的最大值.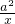 +
+ ≥
≥ ,當且僅當
,當且僅當 =
=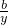 時上式取等號.請利用以上結論,求函數f(x)=
時上式取等號.請利用以上結論,求函數f(x)= +
+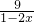 (x∈0,
(x∈0, )的最小值.
)的最小值.查看答案和解析>>
科目:高中數學 來源:2011-2012學年湖南省十二校高三(下)4月聯考數學試卷(理科)(解析版) 題型:解答題
 (θ為參數),求曲線C上的點到直線x-y+1=0的距離的最大值.
(θ為參數),求曲線C上的點到直線x-y+1=0的距離的最大值. +
+ ≥
≥ ,當且僅當
,當且僅當 =
= 時上式取等號.請利用以上結論,求函數f(x)=
時上式取等號.請利用以上結論,求函數f(x)= +
+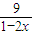 (x∈0,
(x∈0, )的最小值.
)的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com