
如圖,軸截面為邊長為 等邊三角形的圓錐,過底面圓周上任一點作一平面
等邊三角形的圓錐,過底面圓周上任一點作一平面 ,且
,且 與底面所成二面角為
與底面所成二面角為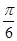 ,已知
,已知 與圓錐側面交線的曲線為橢圓,則此橢圓的離心率為( )
與圓錐側面交線的曲線為橢圓,則此橢圓的離心率為( )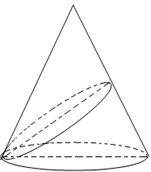
A.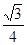 | B. | C. | D. |
 互動英語系列答案
互動英語系列答案科目:高中數學 來源: 題型:單選題
設圓 的圓心為C,A(1,0)是圓內一定點,Q為圓周上任一點.線段AQ的垂直平分線與CQ的連線交于點M,則M的軌跡方程為( ).
的圓心為C,A(1,0)是圓內一定點,Q為圓周上任一點.線段AQ的垂直平分線與CQ的連線交于點M,則M的軌跡方程為( ).
A. | B. |
C. | D. |
查看答案和解析>>
科目:高中數學 來源: 題型:單選題
點 在直線
在直線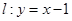 上,若存在過
上,若存在過 的直線交拋物線
的直線交拋物線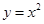 于
于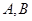 兩點,且
兩點,且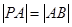 ,則稱點
,則稱點 為“
為“ 點”,那么下列結論中正確的是( )
點”,那么下列結論中正確的是( )
A.直線 上的所有點都是“ 上的所有點都是“ 點” 點” | B.直線 上僅有有限個點是“ 上僅有有限個點是“ 點” 點” |
C.直線 上的所有點都不是“ 上的所有點都不是“ 點” 點” | D.直線 上有無窮多個點是“ 上有無窮多個點是“ 點” 點” |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com