
����С�}�M��12�֣�
����D��ʾ�Ķ����w�У���߅�� ��
�� �������
�������
������ ���C����ֱ��
���C����ֱ�� ƽ��
ƽ�� ��
��
�����O(sh��) ��
�� �քe�Ǿ���
�քe�Ǿ��� ��
�� �����c(di��n)���ھ���
�����c(di��n)���ھ��� ���Ƿ����һ�c(di��n)
���Ƿ����һ�c(di��n) ��ʹֱ��
��ʹֱ�� ƽ��
ƽ�� ��Ո(q��ng)�C����ĽY(ji��)Փ��
��Ո(q��ng)�C����ĽY(ji��)Փ��
��1���C��ԔҊ(ji��n)��������2�����ڣ�M�龀��AB�����c(di��n)�r(sh��)��ֱ��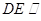 ƽ��
ƽ�� .
.
����ԇ�}��������1���Cֱ����ֱƽ�棬�����Cֱ����ֱƽ���(n��i)�ăɗl�ֱཻ��.�ѽ�(j��ng)�� �ˣ���ô����ƽ���(n��i)��һ�lֱ���cBC��ֱ.��(j��)�}���ã�
�ˣ���ô����ƽ���(n��i)��һ�lֱ���cBC��ֱ.��(j��)�}���ã�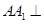 ƽ��ABC������
ƽ��ABC������ .�ɴ˵�
.�ɴ˵� ƽ��
ƽ�� .��2�������B�Y(ji��)
.��2�������B�Y(ji��)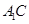 ��ȡ
��ȡ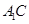 �����c(di��n)O.���]��
�����c(di��n)O.���]�� ��
�� �քe�Ǿ���
�քe�Ǿ��� ��
�� �����c(di��n)�����ھ���
�����c(di��n)�����ھ��� ��ȡ���c(di��n)
��ȡ���c(di��n) ����
����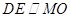 .�Ķ���ֱ��
.�Ķ���ֱ��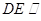 ƽ��
ƽ�� .
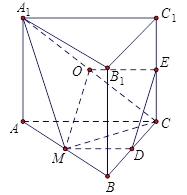
.
ԇ�}������������?y��n)���߅�?img src="http://thumb.zyjl.cn/pic5/tikupic/60/5/ryhdb4.png" style="vertical-align:middle;" />�� ���Ǿ��Σ�
���Ǿ��Σ�
���� .
.
��?y��n)�AB��AC��ƽ��ABC��(n��i)�ăɗl�ֱཻ����
����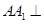 ƽ��ABC.
ƽ��ABC.
��?y��n)�ֱ�� ƽ��ABC��(n��i)������
ƽ��ABC��(n��i)������ .
.
������֪�� ��ƽ��
��ƽ�� ��(n��i)�ăɗl�ֱཻ����
��(n��i)�ăɗl�ֱཻ����
���ԣ� ƽ��
ƽ�� .
.
��2��ȡ����AB�����c(di��n)M���B�� ���O(sh��)O��
���O(sh��)O�� �Ľ��c(di��n).
�Ľ��c(di��n).
����֪��O��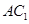 �����c(di��n).
�����c(di��n).
�B��MD��OE���tMD��OE�քe��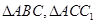 ����λ��.
�����.
���ԣ� ��
��
�B��OM���Ķ���߅��MDEO��ƽ����߅�Σ��t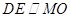 .
.
��?y��n)�ֱ�� ƽ��
ƽ�� ��
�� ƽ��
ƽ�� ��
��
����ֱ��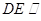 ƽ��
ƽ�� .
.
������AB�ϴ���һ�c(di��n)M������AB�����c(di��n)����ʹ��ֱ��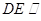 ƽ��
ƽ�� .
.
�����c(di��n)��λ�����gֱ���cƽ���λ���P(gu��n)ϵ.



| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��D. ֱ������ABC ��A1B1C1�У�A1B1= A1C1,�c(di��n)D��E�քe����BC��CC1�ϵ��c(di��n)���c(di��n)D��ͬ���c(di��n)C������AD��DE��F(xi��n)��B1C1�����c(di��n)��
���C����1��ƽ��ADE��ƽ��BCC1B1
��2��ֱ��A1F��ƽ��ADE��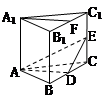
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��D���������F ���c(di��n)
�У��c(di��n) �քe����
�քe����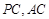 �����c(di��n)��
�����c(di��n)��
(1)���C�� //ƽ��
//ƽ�� ��
��
(2)��ƽ�� ƽ��
ƽ�� ��
�� �����C��
�����C�� ��
��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
�����F �����(c��)ҕ�D����ҕ�D��D��ʾ.�O(sh��)
�����(c��)ҕ�D����ҕ�D��D��ʾ.�O(sh��) ��
��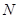 �քe�龀��
�քe�龀�� ��
�� �����c(di��n)��
�����c(di��n)�� �龀��
�龀�� �ϵ��c(di��n)����
�ϵ��c(di��n)���� .
.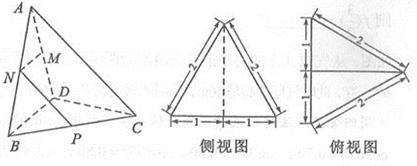
��1���C���� �龀��
�龀�� �����c(di��n)��
�����c(di��n)��
��2�������� ������ֵ.
������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��D�������wABCD��A1B1C1D1�У���(c��)�挦(du��)�Ǿ�AB1��BC1�Ϸքe�Ѓ��c(di��n)E��F(xi��n)����B1E��C1F.���C��EF��ƽ��ABCD.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
�ڎ��wABCDE�У���BAC= ��DC��ƽ��ABC��EB��ƽ��ABC�� AB=AC=BE=2��CD=1.
��DC��ƽ��ABC��EB��ƽ��ABC�� AB=AC=BE=2��CD=1.
��1���O(sh��)ƽ��ABE�cƽ��ACD�Ľ�����ֱ�� �����C��
�����C�� ��ƽ��BCDE��
��ƽ��BCDE��
��2���O(sh��)F��BC�����c(di��n)�����C��ƽ��AFD��ƽ��AFE��
��3������wABCDE���w�e.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��D���������F ������
�У����� �������Σ���(c��)��
�������Σ���(c��)�� �͵���
�͵���  ��
�� ��
�� ��
�� �����c(di��n)����
�����c(di��n)���� ��
�� ���c(di��n)
���c(di��n) ��
��
��1�����C��
 ƽ��
ƽ�� ��
��
��2�������� ������ֵ��
������ֵ�� 
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��D���������FP-ABCD�У� ƽ��ABCD��AD//BC��BC=2AD��
ƽ��ABCD��AD//BC��BC=2AD�� AC��Q�Ǿ���PB�����c(di��n).
AC��Q�Ǿ���PB�����c(di��n).
��1�����C�� ƽ��PAC��
ƽ��PAC��
��2�����C��AQ//ƽ��PCD.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
ABCD�cCDEF�ǃɂ�(g��)ȫ�ȵ������Σ��҃ɂ�(g��)����������ƽ�滥�ഹֱ��M��BC�����c(di��n)���t����ֱ��AM�cDF���ɽǵ�����ֵ�� �� ��
�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | ����p�_�e��(b��o)��(zhu��n)�^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | �����֙�(qu��n)�e��(b��o)��(zhu��n)�^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com