
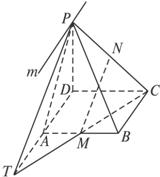
(1)求證:BC∥m;
(2)MN與平面PAD是否平行?試證明你的結(jié)論.
剖析:(1)運(yùn)用線面平行的判定與性質(zhì)定理;
(2)在平面PAD上探尋與直線MN平行的直線.
(1)證明:∵BC![]() 平面PAD,AD
平面PAD,AD![]() 平面PAD,BC∥AD,
平面PAD,BC∥AD,
∴BC∥平面PAD(判定定理).
而BC![]() 平面PBC,平面PBC∩平面PAD=m,
平面PBC,平面PBC∩平面PAD=m,
∴BC∥m(性質(zhì)定理).
(2)解:平行.事實(shí)上,連結(jié)CM并延長,交DA的延長線于T,再連結(jié)PT.
∵M(jìn)是平行四邊形ABCD的邊AB的中點(diǎn),
∴M是TC的中點(diǎn).
∴MN是△TPC的中位線.
∴MN∥PT.
又∵T∈平面PAD,
∴PT![]() 平面PAD.
平面PAD.
∴MN∥平面PAD.
講評:找到平面PAD中的直線PT是解題的關(guān)鍵.實(shí)質(zhì)上這里利用了公理2.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學(xué)生10分鐘應(yīng)用題系列答案
小學(xué)生10分鐘應(yīng)用題系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
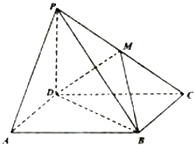 如圖,點(diǎn)P為平行四邊形ABCD外一點(diǎn),且PD⊥平面ABCD,M為PC中點(diǎn).
如圖,點(diǎn)P為平行四邊形ABCD外一點(diǎn),且PD⊥平面ABCD,M為PC中點(diǎn).查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
 如圖所示,P為平行四邊形ABCD所在平面外一點(diǎn),M、N分別為AB、PC的中點(diǎn),平面PAD∩平面PBC=l.
如圖所示,P為平行四邊形ABCD所在平面外一點(diǎn),M、N分別為AB、PC的中點(diǎn),平面PAD∩平面PBC=l.查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com