
偶函數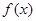 滿足
滿足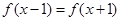 ,當
,當 時,
時, 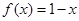 ,則關于
,則關于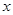 的方程
的方程 在
在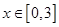 上解的個數是( )
上解的個數是( )
| A.1 | B.2 | C.3 | D.4 |
D
解析試題分析:∵f(x-1)=f(x+1)∴f(x)=f(x+2),
∴原函數的周期T=2,又∵f(x)是偶函數,∴f(-x)=f(x),
又∵x∈[0,1]時,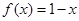 ,函數的周期為2,
,函數的周期為2,
∴原函數的對稱軸是x=1,且f(-x)=f(x+2)。
設y1=f(x) ,y2=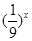 ,方程
,方程 根的個數,即為函數y1=f(x) ,y2= y2=
根的個數,即為函數y1=f(x) ,y2= y2=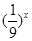 的圖象交點的個數.
的圖象交點的個數.
由以上條件,可畫出y1=f(x) ,y2=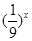 的圖象,
的圖象,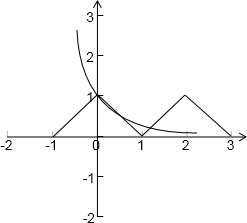
當x=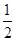 時,y1>y2,當x=1時,y1<y2,
時,y1>y2,當x=1時,y1<y2,
故在(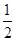 ,1)上有一個交點.
,1)上有一個交點.
結合圖象可得在[0,3]上y1=f(x),y2=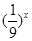 共有4個交點,
共有4個交點,
∴在[0,3]上,原方程有4個根,故選D.
考點:本題主要考查函數的奇偶性、周期性、單調性,函數的圖象,函數零點的概念,一次函數、指數函數的圖象和性質。
點評:難題,本題綜合考查函數的奇偶性、周期性、單調性,函數的圖象,函數零點的概念,一次函數、指數函數的圖象和性質。由已知條件確定函數的性質是解題的關鍵。


湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com