
如圖所示,根據指令(r,![]() )(其中r≥0,-180°<
)(其中r≥0,-180°<![]() ≤180°),機器人在平面上能完成下列動作:先原地旋轉角度
≤180°),機器人在平面上能完成下列動作:先原地旋轉角度![]() (
(![]() 為正時,按逆時針方向旋轉
為正時,按逆時針方向旋轉![]() ;
;![]() 為負時,按順時針方向旋轉-
為負時,按順時針方向旋轉-![]() ),再朝面對的方向沿直線行走距離r.
),再朝面對的方向沿直線行走距離r.

(1)現機器人在直角坐標系的坐標原點,且面對x軸正方向.試給機器人下一個指令,使其移動到點A(4,4).
(2)機器人在完成該指令后,發現在點(17,0)處有一小球正向坐標原點作勻速直線滾動.已知小球滾動的速度為機器人直線行走速度的2倍,若忽略機器人原地旋轉所需的時間,問機器人最快可在何處截住小球?
科目:高中數學 來源: 題型:044
如圖所示,根據指令
(r,θ)(r≥0,-180°≤θ≤180°),機器人在平面上能完成下列動作:先原地旋轉角度
θ(θ為正時,按逆時針方向旋轉θ,θ為負時,按順時針方向旋轉|θ|),再朝其面對的方向沿直線行走距離r.(1)
現機器人在直角坐標系的坐標原點,且面對x軸正方向,試給機器人下一個指令,使其移動到點(4,4).(2)
機器人在完成該指令后,發現在點(17,0)處有一個小球正向坐標原點作勻速直線滾動,已知小球滾動的速度為機器人直線行走速度的2倍,若忽略機器人原地旋轉所需的時間,問機器人最快可在何處截住小球?并給出機器人截住小球所需的指令(結果精確到小數點后兩位).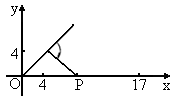
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com