下列結論正確的是 (寫出所有正確結論的序號)
(1)常數列既是等差數列,又是等比數列;
(2)若直角三角形的三邊a、b、c成等差數列,則a、b、c之比為3:4:5;
(3)若三角形ABC的三內角A、B、C成等差數列,則B=60°;
(4)若數列{an}的前n項和為Sn=n2+n+1,則{an}的通項公式an=2n+1.
【答案】
分析:(1)當常數列的項都為0時,是等差數列但不是等比數列;
(2)a,b,c成等差數列⇒
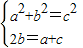
⇒4a=3b,5a=3c⇒a:b:c=3:4:5;
(3)由題意知,A+C=2B,又由內角和為180°,則B=60°;
(4)由數列{a
n}前n項和S
n=n
2+n-1,根據
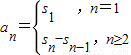
,求得數列{a
n}的通項公式.
解答:解:(1)當常數列的項都為0時,是等差數列但不是等比數列,此命題為假命題;
(2)∵直角三角形的三邊長分別為a,b,c(a<b<c),a,b,c成等差數列,
∴
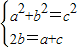
,
∴

,
∴4a=3b,5a=3c,∴a:b:c=3:4:5,故此命題為真命題;
(3)在△ABC中,若三內角A、B、C成等差數列,則A+C=2B,
又由A+B+C=180°,故B=60°,故此命題為真命題;
(4)解:n=1時,a
1=s
1=3,
n≥2時,a
n=s
n-s
n-1=n
2+n+1-[(n-1)
2+n-1+1]=2n,
綜上

,故此命題為假命題.
故答案為 (2)(3)
點評:本題主要考查解三角形問題與等差數列等比數列定義的應用,解決此類問題的關鍵是熟悉有關定義.本題是一個基礎題.

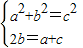 ⇒4a=3b,5a=3c⇒a:b:c=3:4:5;
⇒4a=3b,5a=3c⇒a:b:c=3:4:5;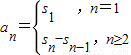 ,求得數列{an}的通項公式.
,求得數列{an}的通項公式.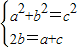 ,
, ,
, ,故此命題為假命題.
,故此命題為假命題.

 同步學典一課多練系列答案
同步學典一課多練系列答案 經典密卷系列答案
經典密卷系列答案 金牌課堂練系列答案
金牌課堂練系列答案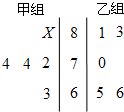 如圖所示莖葉圖記錄了甲乙兩組各5名同學的數學成績.甲組成績中有一個數據模糊,無法確認,在圖中以X表示.若兩個小組的平均成績相同,則下列結論正確的是( )
如圖所示莖葉圖記錄了甲乙兩組各5名同學的數學成績.甲組成績中有一個數據模糊,無法確認,在圖中以X表示.若兩個小組的平均成績相同,則下列結論正確的是( )