
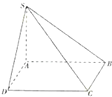
 (2011•許昌三模)已知四棱錐S-ABCD中,AB=BC=CD=DA=SA=2,底面ABCD是正方形,SD=SB=2
(2011•許昌三模)已知四棱錐S-ABCD中,AB=BC=CD=DA=SA=2,底面ABCD是正方形,SD=SB=2| 2 |

| 2 |


| 3 |
| 2 |
| AO2+CO2-AC2 |
| 2×AO×CO |
| 3+3-8 | ||||
2×
|
| 1 |
| 3 |
| 1 |
| 3 |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
| a |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| b |
| π |
| 3 |
| 3 |
| 7 |
| ||
| 7 |
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
 (2011•許昌三模)甲乙兩人進行圍棋比賽,約定每局勝者得1分,負者得0分.比賽進行到有一人比對方多2分或打滿6局時停止,設甲在每局中獲勝的概率為p(p>
(2011•許昌三模)甲乙兩人進行圍棋比賽,約定每局勝者得1分,負者得0分.比賽進行到有一人比對方多2分或打滿6局時停止,設甲在每局中獲勝的概率為p(p>| 1 |
| 2 |
| 5 |
| 9 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com