Question

如果以數列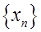的任意連續三項作邊長，都能構成一個三角形，那么稱這樣的數列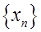為“三角形”數列；又對于“三角形”數列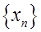，如果函數y=f(x)使得由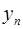=f(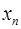)()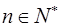確定的數列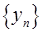仍成為一個“三角形”數列，就稱y=f(x) 是數列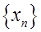的“保三角形”函數。

（Ⅰ）、已知數列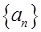是首項為2012，公比為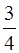的等比數列，求證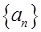：是“三角形”數列；

（Ⅱ）、已知數列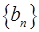是首項為2，公差為1的等差數列，若函數f(x)=  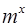(m＞0且m≠1)是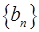的“保三角形”函數. 求m的取值范圍.

 

Answer 1

【答案】

解：（Ⅰ）、是遞減數列···2分，

故對任意的正整數n ，構成三角形當且僅當滿足

這顯然成立，故是“三角形”數列···6分

（Ⅱ）、=7n+1··7分是“三角形”數列

①若0<m<1,則是遞減數列，構成三角形當且僅當滿足    ···6分

②若m>1, 則是遞增數列，可求得···12分。

故m的取值范圍是：或···14分

 

【解析】略